Rhombitruncated Icosahedron

Author

Description

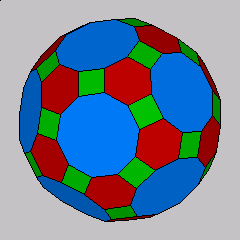
The rhombitruncated icosahedron is one of the thirteen Archimedean solids.

The rhombitruncated icosahedron has 120 vertices, 62 faces and 180 edges. It is generated by truncating the vertices and edges of an icosahedron or of a dodecahedron. Here the distance from vertex to center point is scaled to 1; the edge-length is 2sqrt((31-12sqrt(5))/241).

The coordinates of the rhombitruncated icosahedron where computed with polymake. The planes with normals showing to the icosahedron vertices with distance sqrt((117+48sqrt(5))/241) , the planes with normals showing to dodecahedron vertices with distance sqrt((175+10sqrt(5))/241) and the planes with normals showing to the icosidodecahedron vertices with distance sqrt((179+24qrt(5))/241) to the center point where intersected, the intersection points are the vertices of the rhombitruncated Icosahedron.

Model produced with: JavaView 2.00.005

References

1. H. S. M. Coxeter: Regular Polytopes, Collier-Macmillan Ltd. London (1963).
2. Magnus J. Wenniger: Polyhedron Models, Cambridge University Press (1970).
3. Alan Holden: Shape, Space and Symmetry, Columbia University Press New York/London (1971).
4. Michael Joswig, Ewgenij Gawrilow: Polymake, http://www.math.tu-berlin.de/diskregeom/polymake/doc/.
5. Konrad Polthier and Samy Khadem and Eike Preuss and Ulrich Reitebuch: JavaView Home Page, http://www.javaview.de/.

Files

• Master File: rhombitruncatedicosahedron_Master.jvx
• Applet File: rhombitruncatedicosahedron_Master.jvx
• Preview: rhombitruncatedicosahedron_Preview.gif
• Original File (private file format): rhombitruncatedicosahedron_Original.poly

Submission information

Submitted: Fri Sep 1 16:24:12 MET 2000.
Accepted: Thu Oct 25 14:19:08 MDT 2001.

Author's Address

Technische Universität Berlin
Fachbereich Mathematik, MA 8-5
Straße des 17. Juni 136
D-10623 Berlin, Germany
fuli@sfb288.math.tu-berlin.de
http://www-sfb288.math.tu-berlin.de/~fuli/