

 |
 |
 |
 |
 |
This model simulates the shape of a tight clasp, that is, a ropelength-minimizing configuration of two linked arcs with endpoints fixed in parallel planes. Here, ropelength means the total length of the curves divided by their thickness, the radius of the largest embedded normal tube around them. We use the characterization from [1] of thickness as the infimal radius of circles through three points on the curves.
It is known that thickness equals either the minimum radius of curvature of the curve or the minimum critical self-distance, whichever is less. In particular, a curve of positive thickness is C1,1.
Ropelength minimization is intended as a mathematical model of tying knots tight in real rope. If the radius of the rope is 1, then we assume that the physical rope is the unit normal tube around some core curve K. If this tube is embedded but no larger tube is, then the thickness of K equals 1, and its ropelength is just its length. To minimize ropelength means to use as short a length of such rope as possible.
For two linked loops that remain distance 2 from each other, the length-minimizing configuration is two round circles in perpendicular planes; this was the solution to the Gehring link problem [2]. In [3], we established the existence of C1,1 minimizers for any link type, and gave more examples of tight links. For example, in the tight configuration of a simple linked chain, each component (except at the ends) is a stadium curve, consisting of two semicircles and two straight segments.
The clasp problem asks to minimize the ropelength of a pair of simply linked arcs with free boundary (endpoints) in parallel planes. It seemed natural to expect that in the minimizer the two curves would lie in perpendicular planes, and each would again consist of straight segments and a semicircle. But in work currently underway [4], we establish a balancing criterion for critical points of ropelength; this criterion is not satisfied by that obvious configuration. Indeed it is not hard to exhibit a ropelength-decreasing perturbation. We expect that we will eventually be able to use our balance criterion to get equations describing this tight clasp exactly.
This model presents the results of Evolver [5] simulations of the tight clasp. As described in [6], we fix length and maximize not thickness but a discretization of a smooth energy functional. If we let k(x,y) denote the curvature of the circle through x and tangent to the curve at y, then the reciprocal of thickness is the supremum of k(x,y). Instead of minimizing this supremum, we minimize the Lp norm of k, that is, the integral, over pairs of points x,y on the curves, of k(x,y)p. For p large, minimizers of this energy should approach ropelength minimizers.
The simulation results lead us to conjecture that the minimizing clasp, though necessarily C1,1, by results of [2], has curvature discontinuities not only at the ends of the straight segments, where it jumps from 0 to 1/2 as we had expected, but also near the tips, where the curvature seems to jump from somewhat over 1/2 to exactly 1. We also observe that the geometry near the tips is controlled not by distance to the other strand but instead by the curvature bound. We call such an arc (of constant curvature equal to the bound) a kink; the existence of kinks in some ropelength minimizers like the clasp makes the analysis of the balance criterion [4] significantly more difficult.
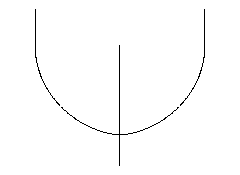
The first image is an orthogonal projection of the clasp, where one strand appears in its exact shape and the other is collapsed to a line.
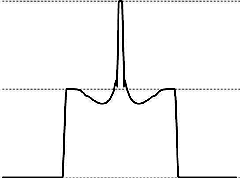
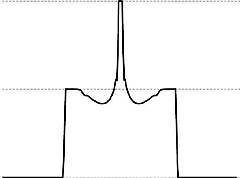
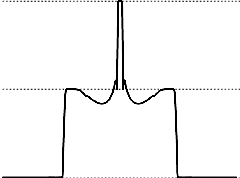
The other three images show graphs of curvature as a function of arclength along one of the arcs of the clasp. We show the graph for the numerical minimizer for three different values of p and n (the number of edges on a polygonal approximation to each arc): p=4096, n=256 and p=8192, n=256 and p=4096, n=512. The close similarity of all three supports the conjecture that this model is a good approximation to the ropelength minimizer or tight clasp.
The dotted horizontal lines show curvature levels 0 and 1/2 and 1 (assuming the clasp has been scaled to have thickness 1). Near the base of each component, there is evidently an arc of a circle of radius 2 around the tip of the other component, while near the tip there is a small arc of a unit circle; this kink is constrained by its own curvature, not by touching the other component.
Limited experimentation suggests that this is indeed the minimizing configuration of the clasp. If we add a twisting perturbation that might allow the two components to have helical segments, this is removed by the gradient descent flow, and the clasp returns to the configuration shown here.
Model produced with: Evolver 2.16
| Keywords | thick knots; minimum ropelength | |
| MSC-2000 Classification | 57M25 (49Q10, 53A04) | |
| Zentralblatt No. | 05264884 |
The original file is a Surface Evolver .fe file, but requires a not-yet-released version of Evolver that includes the new knot thickness energies. The first image is an orthogonal projection of the clasp; the other three are graphs of curvature as a function of arclength along the strand of the clasp.
Submitted: Thu Nov 15 7:39:57 CET 2001.
Revised: Tue Feb 11 15:00:29 CET 2003.
Accepted: Sun May 25 18:34:39 CET 2003.
University of Illinois, Department of Mathematics
1409 W Green St
Urbana, IL, USA 61801-2975
jms@uiuc.edu
http://torus.math.uiuc.edu/jms/