Trefoil Knot

Author

Description

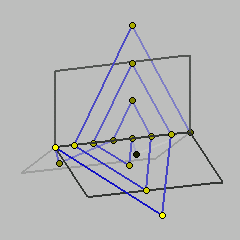
This is the simplest 3-page diagram of knot 3_1 (the trefoil knot).

This is the simplest non-trivial knot. Its simplest planar diagram has 3 crossings. A list of other knots with small crossing number can be found in [1] and [2]. 3_1 is an alternating knot. It is chiral and invertible. It is also the torus knot of type (2,3). Here we give the simplest 3-page diagram of the trefoil knot. It has 8 vertices. 3-page diagrams were introduced in [3]. According to the notation given in [3] this diagram is encoded by the word a_1a_0a_0d_2d_1c_0c_0c_2.

References

1. D. Rolfsen: Knots and Links, Publish or Perish, Houston (1990).
2. C. Cerf: Atlas of oriented knots and links, http://at.yorku.ca/t/a/i/c/31.dir/cerf.htm.
3. I. Dynnikov: Three-page approach to knot theory. Encoding and local moves, Functional Analysis and Its Appl. 33, 4 (1999), 260--269.
4. I. Dynnikov: Three-page approach to knot theory. Universal semigroup, Functional Analysis and Its Appl. 34, 1 (2000), 24--32.

Files

• Master File: TrefoilLeft_Master.jvx
• Applet File: TrefoilLeft_Applet.jvx
• Preview: TrefoilLeft_Preview.gif
• Other: TrefoilLeft_Other.jkb

Submission information

Submitted: Sun Sep 10 07:10:24 CET 2000.
Accepted: Mon Nov 20 17:06:57 CET 2000.

Author's Address

Moscow State University
Department of Mechanics and Mathematics
Vorobyovy gory
Moscow 119899
Russia
dynnikov@mech.math.msu.su
http://mech.math.msu.su/~dynnikov