Cubeoctahedron

Author

Description

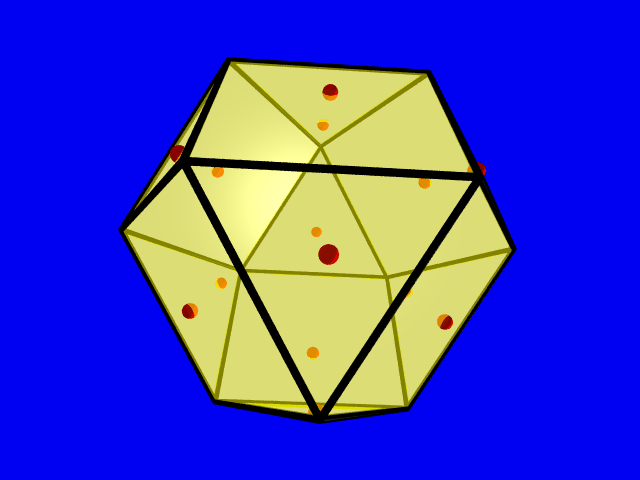
Densest lattice packing of a cubeoctahedron

The cubeoctahedron has 12 vertices, 24 edges and 14 facets, 6 squares and 8 triangles. It is one of the thirteen Archimedean solids and it is the difference body of a tetrahedron. Its dual is called rhombic dodecahedron. It was already mentioned by Plato and rediscovered during the 15th century by the outstanding artist Piero della Francesca.

In 1972 Hoylman calculated the lattice packing density of a cubeoctahedron, which is equal to 45/49=0.9183... The 14 points in the picture show the lattice points of a critical lattice lying in the boundary.

Model produced with: JavaView v2.00.a11

References

1. Ulrich Betke and Martin Henk: Densest lattice packings of 3-polytopes, Comp. Geom. 16 , 3 (2000), 157 - 186.
2. D.J. Hoylman: The densest lattice packing of tetrahedra, Bull. Amer. Math. Soc 76 (1970), 135 - 137.

Files

• Master File: cubeoctahedron_Master.jvx
• Applet File: cubeoctahedron_Master.jvx
• Preview: cubeoctahedron_Preview.gif

Gif-file was produced by Povray 3.02

Submission information

Submitted: Thu Feb 1 16:41:52 CET 2001.
Accepted: Fri Apr 27 14:11:54 CET 2001.

Author's Address

University of Magdeburg
Department of Mathematics
Universitätsplatz 2
D-39106 Magdeburg
henk@mail.math.uni-magdeburg.de
http://www.math.uni-magdeburg.de/~henk