

 |
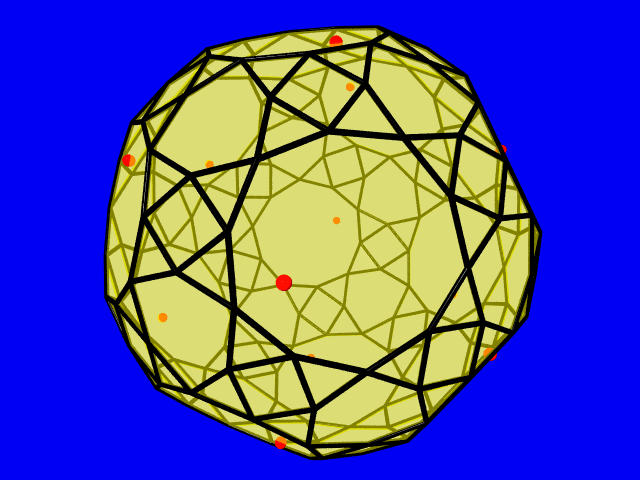 |
Densest lattice packing of a snub dodecahedron
The snub dodecahedron has 60 vertices, 150 edges and 92 facets, 12 pentagons and 80 triangles. It is one of the thirteen Archimedean solids and its dual is called pentagonal hexecontahedron. It was rediscovered by Johannes Kepler and a drawing can be found in his 1619 book Harmonice Mundi.
The density of a densest lattice packing was calculated with the algorithm of Betke and Henk. Since the snub dodecahedron is a non 0-symmetric polytope one first has to compute the difference body of a snub cube, which is a 0-symmetric polytope with 180 vertices, 360 edges and 182 facets, 12 decagons, 20 hexagons, 30 squares and 120 triangles. It is shown in the second picture.
The optimal packing lattices of a convex body and its difference body coincide. The lattice packing density of a snub dodecahedron is equal to 0.7886..., and the 12 points in the picture show the lattice points of a critical lattice of the difference body lying in the boundary.
Model produced with: JavaView v2.00.a11
| Keywords | lattice packings; polytopes; packings; critical lattice; snub dodecahedron | |
| MSC-2000 Classification | 52C17 (11H31) | |
| Zentralblatt No. | 01683001 |
Gif-file was produced by Povray 3.02
Submitted: Thu Feb 1 16:41:52 CET 2001.
Accepted: Fri Apr 27 14:11:54 CET 2001.
University of Magdeburg
Department of Mathematics
Universitätsplatz 2
D-39106 Magdeburg
henk@mail.math.uni-magdeburg.de
http://www.math.uni-magdeburg.de/~henk