

 |
 |
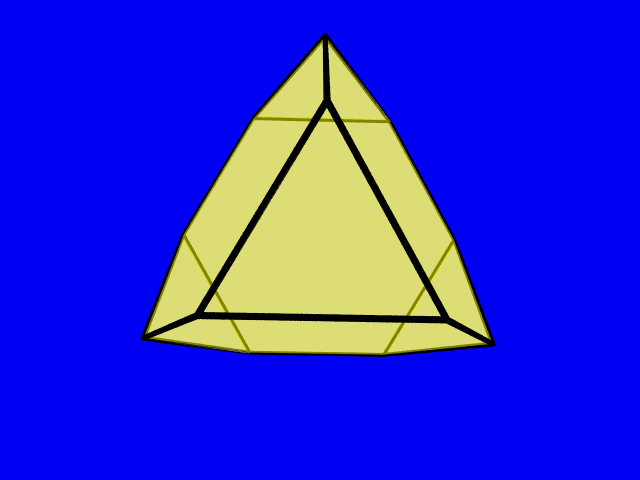
Densest lattice packing of a truncated tetrahedron
The truncated tetrahedron has 12 vertices, 18 edges and 8 facets, 4 hexagons and 4 triangles. It is one of the thirteen Archimedean solids and its dual is called trikis tetrahedron. It was rediscovered during th 15th century by the outstanding artist Piero della Francesca.
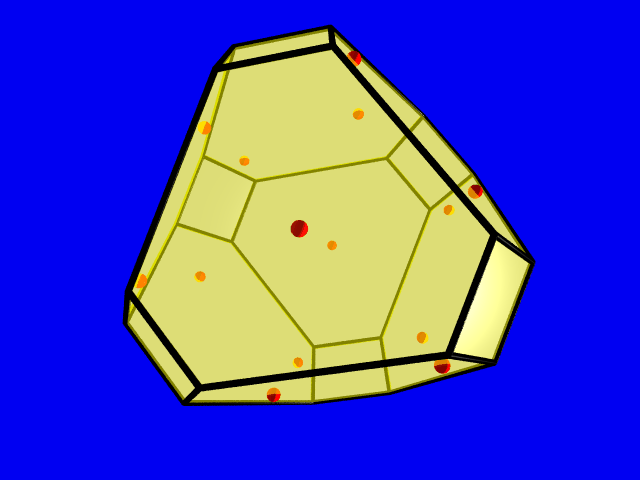
The density of a densest lattice packing was calculated with the algorithm of Betke and Henk. Since the truncated tetrahedron is a non 0-symmetric polytope one first has to compute the difference body of a truncated tetrahedron, which is a 0-symmetric polytope with 24 vertices, 36 edges and 14 facets, 8 hexagons and 6 squares. It is shown in the second picture.
The optimal packing lattices of a convex body and its difference body coincide. The density of a truncated tetrahedron is equal to 0.6809..., and the 14 points in the picture show the lattice points of a critical lattice of the difference body lying in the boundary.
Model produced with: JavaView v2.00.a11
| Keywords | lattice packings; polytopes; packings; critical lattice; truncated tetrahedron | |
| MSC-2000 Classification | 52C17 (11H31) | |
| Zentralblatt No. | 01683009 |
Gif-file was produced by Povray 3.02
Submitted: Thu Feb 1 16:41:52 CET 2001.
Accepted: Fri Apr 27 14:11:54 CET 2001.
University of Magdeburg
Department of Mathematics
Universitätsplatz 2
D-39106 Magdeburg
henk@mail.math.uni-magdeburg.de
http://www.math.uni-magdeburg.de/~henk