

 |
A 6-dimensional point configuration and a triangulation of it with no flips.
In [2] Santos constructed a 6-dimensional point configuration that has a triangulation without flips. The configuration consists of 384 points, and the explicitly constructed triangulation has 25920 simplices. The proof that this triangulation has no flips uses new sophisticated tools developed by Santos.
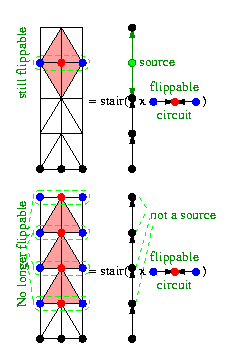
One of the concepts of preventing flips is illustrated in the sketch: The product of two triangulations (which is not a triangulation) can be refined to the so-called staircase-triangulation according to orientations of the one-skeletons of the factors. One building block in Santos' construction is roughly the following: If one factor has an orientation with neither sources nor sinks then a flippable circuit in the other factor is no longer flippable in the staircase triangulation of the product according to the given orientations. (The sketch in dimension two can only depict the influence of sources.)
This model provides the data necessary to check the correctness of Santos' construction in an elementary fashion by computer. This was successfully done already by the triangulation program TOPCOM [1], which is applicable to any point configuration that is not too large.
It may be interesting to investigate whether there is a point configuration in general position allowing for a triangulation without flips. Along this line the model may be especially useful.
Model produced with: TOPCOM 0.5.5
| Keywords | Triangulation of a Point Configuration; Flip | |
| MSC-2000 Classification | 52B12 (52B11, 52C40, 52C22) | |
| Zentralblatt No. | 01682992 |
Submitted: Tue Aug 1 15:01:36 CET 2000.
Accepted: Mon Nov 20 17:06:57 CET 2000.
Konrad-Zuse-Zentrum für Informationstechnik Berlin
Takustr. 7
14195 Berlin
Germany
rambau@zib.de
http://www.zib.de/rambau