A Neighborly Cubical 4-Polytope

Authors

Description

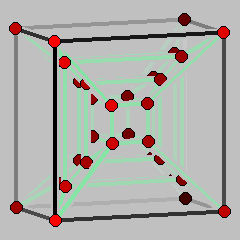
A cubical 4-polytope with the graph of the 5-dimensional cube.

In [4] we showed that for arbitrary n>d there is a cubical d-polytope, which arises as a projection of a combinatorial n-cube, and whose [d/2-1]-skeleton is isomorphic to the [d/2-1]-skeleton of the n-dimensional cube. This solves a problem of Babson, Billera, and Chan [1].

The polytope whose Schlegel diagram is shown here is a member of this 2-parameter family where d=4 and n=5. Examples with d=2 and arbitrary n>2 have been constructed before by Goldfarb [3].

Model produced with: polymake 1.3.1

References

1. Eric K. Babson, Louis J. Billera, and Clara S. Chan: Neighborly cubical spheres and a cubical lower bound conjecture, Israel J. Math. 102 (1997), 297-315.
2. Ewgenij Gawrilow and Michael Joswig: polymake, http://www.math.tu-berlin.de/diskregeom/polymake.
3. Donald Goldfarb: On the complexity of the simplex algorithm, in Advances in optimization and numerical analysis, Proc. 6th Workshop on Optimization and Numerical Analysis, Oaxaca, Mexico, January 1992, Kluwer (1994), 25-38.
4. Michael Joswig and Günter M. Ziegler: Neighborly cubical polytopes, Discrete Comput. Geometry, to appear.

Files

• Master File: C45_Master.poly
• Applet File: C45_Applet.jvx
• Preview: C45_Preview.gif

Submission information

Submitted: Mon May 1 09:32:05 CET 2000.
Accepted: Mon Nov 20 17:06:57 CET 2000.

Authors' Addresses

TU Berlin
Sekr. MA 7-1
Straße des 17. Juni 136
10623 Berlin
Germany
joswig@math.tu-berlin.de
http://www.math.tu-berlin.de/~joswig

TU Berlin
Sekr. MA 7-1
Straße des 17. Juni 136
10623 Berlin
Germany
ziegler@math.tu-berlin.de
http://www.math.tu-berlin.de/~ziegler