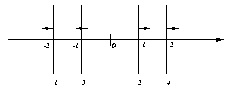Examples for generalized antiweb-facets

Author

Description

This is an example for the occurrence of generalized antiweb facets.

We give a very short overview of the terms necessary to understand the examples. For details see the references.

Given an infeasible inequality system S: Ax <= b, consider the feasible subsystems polytope P_FS, which is the convex hull of the incidence vectors of all feasible subsystems. An irreducible inconsistent subsystem (IIS) of this infeasible system is a subsystem, such that each proper subsystem of it is feasible. Clearly, the feasible subsystems of S form an independence system. The IISs are the circuits of this independence system.

Laurent [2] introduced generalized antiwebs and investigated under which circumstances facets of the corresponding independence system polytope arise from these structures.

Let m, t, q be integers such that 1 <= q <= t <= m, let E={0, ... , m-1} be a finite set, and define for each i in M:={0, ... , m-1} the subset E_i={i, ..., i+t-1} (calculated modulo m), formed by t consecutive elements of E. A (m,t,q)-generalized antiweb on E is the independence system having the following family of subsets of E as circuits:

AW(m,t,q) = {C : C is a subset of E_i for some i in M, |C| = q}.

Amaldi, Pfetsch, Trotter [1] investigate for which parameters m,t,q the independence system arising from AW(m,t,q) is the independence system of feasible subsystems of an infeasible linear inequality system Ax <= b. Furthermore the cases where facets arise from generalized antiwebs as induced substructures are discussed. The following propositions are obtained:

Proposition: The sets in AW(m,t,q) correspond to the IISs of an infeasible linear inequality system Ax <= b with m inequalities if and only if

• t=q and

• t = m-2 or
• t = m

Proposition: Let S: Ax <= b be an infeasible linear inequality system with m inequalities. Let AW(m,t,q) correspond to the IISs of S. The inequality x₁+x₂+ ... +x_m <= floor(m(q-1)/t) defines a facet for P_FS if and only if

• t=q and

• t=m or
• t = m-2 and t not equal to 2.

The example aw.4.2 is the case m=4, t=q=2. The infeasible inequality system in file aw.4.2.lp (in lp-format) has AW(4,2,2) as IISs. The file aw.4.2.eps contains a picture in postscript. The corresponding polytope P_FS is contained in the file aw.4.2.poly (in polymake-format), including the list of facets. You can see that no facet like above arises.

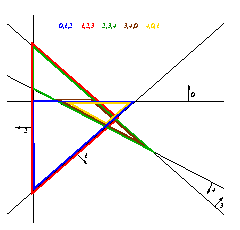
The example aw.5.2 is the case m=5, t=q=3. Again the example in file aw.5.3.lp has AW(5,3,3) as its IISs and a picture is given in aw.5.3.eps. The IISs are given in different colors. The colored triangles mark the triangles involved in each IIS. The file aw.5.3.poly gives P_FS and its facets.

Model produced with: Polymake 1.4

References

1. Edoardo Amaldi, Marc E. Pfetsch, Leslie E. Trotter, Jr.: On the Maximum Feasible Subsystem Problem, IISs and IIS-hypergraphs, preprint.
2. Monique Laurent: A generalization of antiwebs to independence systems and their canonical facets, Math. Prog. 45 (1989), 97 -- 108.

Files

• Master File: aw.4.2.poly
• Master File: aw.5.3.poly
• Preview: aw.4.2.gif
• Preview: aw.5.3.gif
• Other: aw.4.2.lp
• Other: aw.5.3.lp
• Other: aw.4.2.eps
• Other: aw.5.3.eps

Submission information

Submitted: Sun Sep 10 07:10:24 CET 2000.
Accepted: Mon Nov 20 17:06:57 CET 2000.

Author's Address

Technische Universität Berlin
Fachbereich Mathematik, MA 7-1
Straße des 17. Juni 136
10623 Berlin, Germany
pfetsch@math.tu-berlin.de
http://www.math.tu-berlin.de/~pfetsch