Goldfarb's Cube

Author

Description

A class of linear programs for which the Shadow Vertex Simplex Algorithm requires an exponential number of steps.

The Simplex Method due to Dantzig is one of the most important algorithms to solve linear optimization problems, see Schrijver [3, Chapter 11]. It walks along ascending edges from an arbitrary vertex of the polyhedron described by a set of linear inequalities to an optimal vertex. At each sub-optimal vertex one needs to make a decision on how to proceed: Which one among the better neighbors should be chosen? An algorithm to solve this problem is called a pivoting strategy. One major open question is whether there exists a pivoting strategy which makes the Simplex Method a polynomial time algorithm, even in the worst case. Up to now, for each of the many pivoting strategies suggested in the literature there seems to be a class of counter-examples, which are bad. That is to say, the Simplex Method with the pivoting strategy in question has super-polynomial running time on the respective input. Strangely enough, most of the inequality systems which turn out to be difficult for the Simplex method are combinatorially equivalent to the cube.

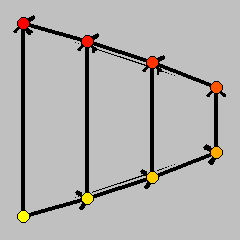
In this model, we are focussing on the Shadow Vertex Pivoting Strategy. The first construction of bad examples for this algorithm is due to Goldfarb. Here we use the description as a deformed product due to Amenta and Ziegler.

For e<1/2 and g<=1/4e we obtain a linear program:

max x_d

0	<=	x1	<=	1
e x1	<=	x2	<=	1 - e x1
e xk - e g xk-1	<=	xk+1	<=	1 - e xk + e g xk-1	, where 2 <= k < d.

The set of admissible solutions is a d-dimensional combinatorial cube, the Goldfarb d-cube. Projecting the Goldfarb d-cube onto the plane spanned by the last two unit vectors leaves all the vertices visible. This yields a 2^d-gon such that the linear objective function x_d on the cube induces an ascending path through all the vertices of the projection.

Substituting g=0 in the above inequality description of the cubes, we obtain the Klee-Minty cubes, see Schrijver [3, 11.4]. Substituting e=0 and g=0 yields the usual 0/1-cube.

Model produced with: polymake 1.3.2

References

1. Nina Amenta and Günter M. Ziegler: Deformed products and maximal shadows of polytopes, Contemporary Math. 233 (1999), 57-90.
2. Donald Goldfarb: On the complexity of the simplex algorithm, in Advances in optimization and numerical analysis, Proc. 6th Workshop on Optimization and Numerical Analysis, Oaxaca, Mexico, January 1992, Kluwer (1994), 25-38.
3. Alexander Schrijver: Theory of Linear and Integer Programming, Wiley-Interscience (1986).

Files

• Master File: Goldfarb3.poly
• Applet File: Goldfarb3.jvx
• Preview: Goldfarb3.gif

Submission information

Submitted: Sun Sep 10 07:10:24 CET 2000.
Accepted: Mon Nov 20 17:06:57 CET 2000.

Author's Address

Technische Universität Berlin
Fachbereich Mathematik, MA 7-1
Straße des 17. Juni 136
10623 Berlin, Germany
joswig@math.tu-berlin.de
http://www.math.tu-berlin.de/~joswig