

 |
 |
M. Perles [2] conjectured that the facet subgraphs of a simple convex d-dimensional polytope are exactly the (d-1)-regular, connected, induced, non-separating subgraphs. The conjecture does hold for dimension three and smaller. However, Christian Haase and Günter M. Ziegler [1] proved that the conjecture does not hold in dimension four or greater. Based on their ideas we constructed a counterexample in dimension 4, which, however is smaller than the original construction. Counterexamples in higher dimensions may be obtained by wedging [1].
The counterexample presented here (perles.poly) is a simple 4-polytope with 2592 vertices and 529 facets. The 3-regular, connected, induced, non-separating subgraph which does not correspond to a facet has 1076 nodes. The construction of Haase and Ziegler [1] (and the one presented here) actually produces a counterexample to the dual version of the weak Perles conjecture in dimension 4. Therefore the applet (figure 1) illustrates the dual case: it depicts a modification of Bing's House, a 2-complex without a free edge and without 2-dimensional homology. The core idea of Haase and Ziegler is to embed Bing's House into the boundary complex of the simplicial counterexample.
Definition: A simplicial d-polytope satisfies the weak Perles conjecture if the vertex stars are the only pure (d-1)-dimensional, dually (d-1)-connected, non-separating subcomplexes of its boundary for which every maximal simplex has one free facet.
Haase and Ziegler [1] observed that for any (simplicial) 4-dimensional counterexample Q to the dual version of the weak Perles conjecture, the boundary of Q contains a 2-complex without a free edge, and without 2-dimensional homology. Examples of such complexes are known and in the following a modification of Bing's House is used to construct the counterexample.
This modification of Bing's House consists of two rooms, the UpperRoom and the LowerRoom, where each of them is connected to the outside via a `chimney' through the other room (figure 1). The modified Bing's House can be embedded in a pile of 2*3*4 cubes, triangulated as follows: Each cube is split into 6 tetrahedra, and the tetrahedra are all grouped around one of the diagonal axes of the cube. Add a cone over the boundary with apex w to get a simplicial 3-sphere C. The complex C is the boundary complex of a simplicial 4-polytope Q and C contains a triangulation of the modified Bing's House as a subcomplex. In the following C will refer to the whole complex and B will refer to the subcomplex representing Bing's House. Now the construction proceeds in a series of stellar subdivisions on edges of C. Essentially these subdivisions ensure that B becomes an induced subcomplex and that C is `finely' triangulated: The subcomplex which in the end will disprove the Perles conjecture will be composed of partial vertex stars (of vertices in B) covering B. (Each triangle of B is contained in exactly two of the chosen partial vertex stars whose intersection lies entirely in B.) Each tetrahedron of this subcomplex must have exactly one free triangle, so the triangulation must be fine enough to ensure that any two of the chosen partial vertex stars do not intersect outside B.
In order to find the subcomplex in question, Haase and Ziegler [1] give a coloring of the vertices of B such that the color of a vertex determines which part of its vertex star (the part lying in the UpperRoom, the part lying in the LowerRoom or the part which lies in none of the rooms) is added to the subcomplex.
Finally we have to construct Q, a 4-polytope with the same combinatorics as C. This process of `lifting' C into R4 is done as follows:
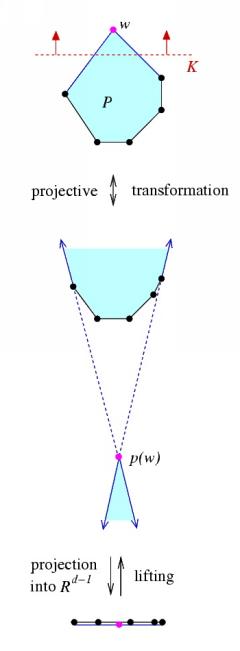
For a given d-polytope P consider the following operation: transform P projectively by moving a hyperplane to `infinity' which separates one vertex w of P from the others. So, if the halfspace H defined by H := {x in Rd : ax + ad+1 > 0} contains all vertices of P except w and is bounded by the hyperplane K := {x in Rd : ax + ad+1 = 0}, we define the projective transformation p as p(x) := x / (ax + ad+1) , x in Rd\K. This is not an admissible projective transformation for P, in particular it is not even defined on all of P. The image p(P\K) is a union of two unbounded polyhedra, the edges incident to w become rays and the lines they determine all intersect in p(w). Now we remove the last coordinates from the vertices in p(P\K) but keep the combinatorial information of P; we end up with a (d-1)-sphere projected to Rd-1 with the same combinatorics as P (see figure 2).
The aim is to reverse this process: Starting with C we try to find fourth coordinates for its vertices such that we get Q after a projective transformation with a hyperplane separating the apex w from the other vertices.
In the construction of C we start with the triangulated pile of 2*3*4 cubes described above. The vertices of the cubical complex lie in Z3. After adding the cone over the boundary with apex w and completing all stellar subdivisions the solution of a linear program yields fourth coordinates for the vertices of C. In this instance, the linear program was solved with CPLEX and the solution was checked for feasibility afterwards. The resulting embedding of C in R4 has the property that after removing all the facets containing w the remaining complex is embedded on a convex surface U, all the facets containing w are embedded on a cone (with apex w) and the cone lies below U. One may imagine this situation as a bowl U sitting in a cone. In figure 2 the bowl U corresponds to the black lines, the cone to the (dashed and solid) blue ones. Finally the lifted complex has to be projectively transformed by moving a hyperplane separating the apex w from the other vertices to infinity to obtain Q.
At the end of their paper Haase and Ziegler [1] ask whether the facet subgraphs of a simple 4-polytope are exactly the 3-regular, 3-connected, induced, non-separating and planar subgraphs. For the example presented here, Petra Mutzel (Technical University Vienna) kindly examined the subgraph in question and proved its non-planarity. This is not surprising, since the subgraph (with its embedding) is a triangulation of Bing's House. Therefore this example is not a counterexample to the proposed question.
In the following the content of perles.poly is described briefly. The two sections which determine the counterexample are VERTICES and the non standard section SUBGRAPH_NODES containing the vertices which induce the 3-regular, 3-connected and non-separating subgraph which does not correspond to a facet. Any further section can be computed from this information, for example by polymake, though computation might take some time. Therefore some additional sections are included in the file. In the following a complete list of the sections in perles.poly:
standard sections: VERTICES, BOUNDED, CENTERED, FACETS, VERTICES_IN_FACETS, GRAPH, DIM, AMBIENT_DIM, SIMPLE, F_VECTOR, F2_VECTOR.
non standard sections: SUBGRAPH_NODES (the vertices inducing the subgraph), SUBGRAPH, COMPL_SUBGRAPH (the subgraph induced by the complementary set of vertices), SUBGRAPH_CONNECTIVITY, COMPL_SUBGRAPH_CONNECTIVITY.
| Keywords | polytope, reconstructions, Perles conjecture, simplicial complex, lifting | |
| MSC-2000 Classification | 52B11 | |
| Zentralblatt No. | 05264890 |
Submitted: Wed Mar 27 16:03:39 CET 2002.
Revised: Tue Nov 5 16:55:33 CET 2002.
Accepted: Wed Jan 29 12:17:06 CET 2003.
TU Berlin
Fakultät 2, Institut für Mathematik, MA 6-2
Strasse des 17. Juni 136
10623 Berlin, Germany
witte@math.tu-berlin.de