

 |
 |
 |
A cubical 4-polytope with an odd number of facets and a dual Boy's surface.
It has been observed by Stanley and by MacPherson that every cubical d-polytope determines a PL immersion of an abstract cubical (d-2)-manifold into (the barycentric subdivision of) the boundary of the polytope [1]. In the case of cubical 4-polytopes each connected component of the dual manifold is a surface (a compact 2-manifold without boundary).
We prove in [3] that every normal crossing codimension one immersion of a compact 2-manifold into R3 is PL-equivalent to a dual manifold immersion of a cubical 4-polytope. Thus, in particular non-orientable dual 2-manifolds do arise: In [4] we described a rather small and simple instance of a 4-polytope with a non-orientable dual 2-manifold (one component is a Klein bottle). If the dual two-manifold has odd Euler characteristic (with an odd number of non-orientable components of odd genus), the resulting cubical 4-polytope has an odd number of facets.
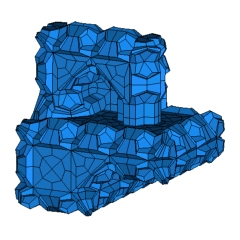
Here we present an example of a cubical 4-polytope with an odd number of facets, which has Boy surface (an immersed projective plane with a single triple point) as a dual manifold immersion. This solves problems of Eppstein, Thurston and others [2]. Our explicit example has 17,718 vertices and 16,533 facets. From this example, it follows in particular that every combinatorial cube has a subdivision into an even number of cubes (without subdividing the boundary). Moreover, it yields that for any geometric hexa mesh the flip graph (see Bern et al. [2]) has at least two connected components.
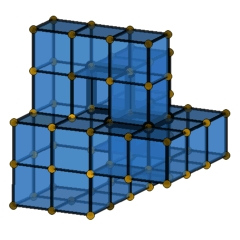
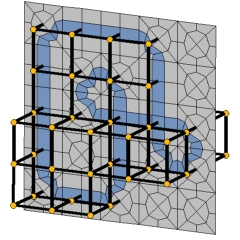
Our figures represents the key ideas for the construction: For a
given, small (74 vertices) lattice version of Boy's surface, one produces
a regular subdivision for a "pile of cubes" that has a subdivision of
the Boy surface as a dual manifold. The result (file C4P_Boy_C3B_with_dual_Boy_surface.hexas)
is then lifted to a
4-polytope by a prism-type construction. (See [3] for details.)
The existence of cubical d-polytopes with an odd number of facets is governed by subtle topological data/obstructions. In particular, such polytopes exist for d=3 (easy) and d=4 (presented here), but not for d=6,8,9 or 10. The cases d=5 and d=7 remain open, for now.
Our submission includes the regular subdivision for a "pile of cubes" that has a subdivision of
the Boy surface as a dual manifold (file C4P_Boy_C3B_with_dual_Boy_surface.hexas).
Furthermore, we provide our set of "templates" used to construct this regular cubical 3-ball:
For each possible type of a vertex star of a normal-crossing grid immersion of a surface (compare the image files "template_*_vertexstar.jpg"), the set of templates
contains a regular cubical subdivision of the standard cube with a dual manifold PL-isomorphic to the vertex star
of the grid immersion. This set of templates can be used to produce cubical 4-polytopes with prescribed dual manifold immersion [3, Thm. 7.3]. (Consider the C4P_Boy_readme.txt for a description of the file format.)
The cubicality of the 4-polytope C4P_Boy_Master.poly can be verified using polymake 2.1 and polymake rules file c4p.rules.
Model produced with: polymake 2.1
| Keywords | cubical complexes; cubical polytopes; regular subdivision; normal crossing codimension one PL immersion; Boy's surface; grid immersion | |
| MSC-2000 Classification | 52B12 (52B11, 52B05) | |
| Zentralblatt No. | 05264900 |
Submitted: Tue Jul 13 11:37:01 CEST 2004.
Revised: Mon Jul 4 12:20:08 CEST 2005.
Accepted: Tue Jul 26 12:12:12 MET DST 2005.
TU BerlinGünter M. Ziegler
Inst. Mathematics, MA 6-2
Strasse des 17. Juni 136
10623 Berlin
Germany
schwartz@math.tu-berlin.de
http://www.math.tu-berlin.de/~schwartz
TU Berlin
Inst. Mathematics, MA 6-2
Strasse des 17. Juni 136
10623 Berlin
Germany
ziegler@math.tu-berlin.de
http://www.math.tu-berlin.de/~ziegler