Smallest non-trivial 2s2s-polytope

Author

Description

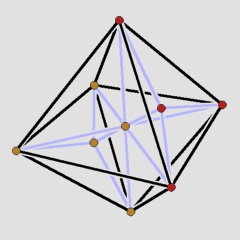
The smallest non-trivial 2-simplicial and 2-simple 4-polytope.

A polytope P is k-simplicial if all its k-faces are simplices and it is h-simple if its dual polytope P^Δ is h-simplicial [2]. Therefore, a 4-dimensional polytope is 2-simplicial and 2-simple, if all 2-dimensional faces are triangles and all edges are contained in exactly 3 facets; in this case, we call it a 2s2s-polytope. Trivially, the 4-simplex is a 2s2s-polytope.

The flag vectors of 2s2s-polytopes satisfy two linear inequalities, valid for all flag vectors of 4-polytopes, with equality and hence are contained in a 2-dimensional face of the flag vector cone of 4-polytopes [1]. It was first shown by Paffenholz and Ziegler [5] that there exist infinitely many 2s2s-polytopes on an arbitrarily large number of vertices.

It is then natural to ask for the existence of 2s2s-polytopes on few vertices. The polytope W₉ on 9 vertices, of which a Schlegel diagram is given in the first figure, is the combinatorially unique smallest non-trivial 2s2s-polytope.

This can be proved by elementary methods in several steps. Let P be a 2s2s-polytope with at most 9 vertices that is not the simplex; then one can show:

• P cannot have less than 9 vertices.
• P contains at most one facet with 6 vertices.
• if P contains an octahedron then it is combinatorially equivalent to W₉.
• P or P^Δ contains an octahedron.
• W₉ is self-dual.

The polytope given here generalises to a whole family of 2s2s-polytopes with a further, very interesting property. A d-polytope is elementary if it satisfies g₂=0, where

g₂ = f₀₂ - 3 f₂ + f₁ - d f₀ + d(d+1)/2

with the (reduced) flag vector (f₀,f₁,f₂;f₀₂). Kalai [3] showed that g₂>=0 is a valid linear inequality for all flag vectors of 4-polytopes. Elementary 2s2s-polytopes can therefore be found on a ray l₁ of the flag vector cone (see [1]).

Until recently, only two flag vectors of polytopes were known to lie on l₁. The polytope W₉ is elementary, which can be easily calculated from its f-vector (9,26,26,9) and from the fact that it is 2-simplicial (i.e. f₀₂=3f₂). By performing a sequence of "pseudo-stacking steps", that is, placing new vertices beyond certain facets in a suitable way, one can construct elementary 2s2s-polytopes W_4k+1 on 4k+1 vertices for all k>=1. The construction is described in detail in [4], together with other examples that cover all vertex numbers n>=9, n≠12.

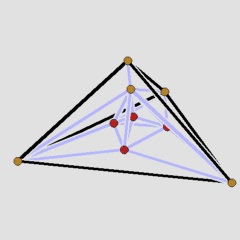
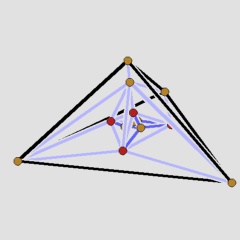
The second figure shows a different Schlegel diagram of W₉. Pseudo-stacking starts beyond the simplex facet, whose vertices are coloured red in all the figures, and adds four vertices. This yields the next example, W₁₃, depicted in the third figure, with new edges arising in the pseudo-stacking process hilighted.

References

1. Bayer, Margaret M.: The Extended f-Vectors of 4-Polytopes, J. Combin. Theory Ser. A 44 (1987), 141--151.
2. Grünbaum, Branko: Convex Polytopes, 2nd edition, Prepared and with a preface by Volker Kaibel, Victor Klee and Günter M. Ziegler, Springer-Verlag (2003).
3. Kalai, Gil: Rigidity and the lower bound theorem. I, Invent. Math. 88 (1987), 125--151.
4. Paffenholz, Andreas and Werner, Axel: Constructions for 4-Polytopes and the Cone of Flag Vectors, Cont. Math. 423 (2007), 283--303, http://de.arxiv.org/abs/math.CO/0511751.
5. Paffenholz, Andreas and Ziegler, Günter M.: The E-construction for lattices, spheres and polytopes, Discrete Comput. Geom. 32 (2004), 601--621.

Files

• Master File: W9.poly
• Applet File: W9_symm.jvx
• Applet File: W9.jvx
• Applet File: W13.jvx
• Preview: W9_symm.jpg
• Preview: W9.jpg
• Preview: W13.jpg

Submission information

Submitted: Wed Dec 14 15:51:58 CET 2005.
Revised: Mon Mar 19 16:51:00 CET 2007.
Accepted: Tue Jun 5 12:50:52 CEST 2007.

Author's Address

TU Berlin
Inst. f. Mathematik, MA 6-2
Str. des 17. Juni 136
10623 Berlin
Germany
awerner@math.tu-berlin.de