

 |
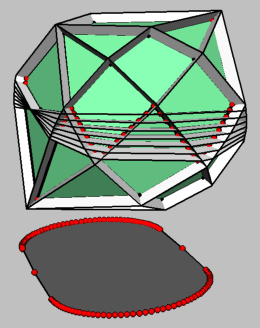
| Figure 1: Dual zonotope with 2D-shadow |
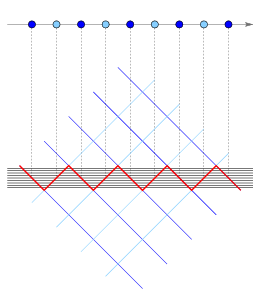 |
| Figure 2: Affine 1D- and 2D-arrangement |
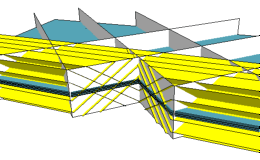 |
| Figure 3: Affine 3D-arrangement |
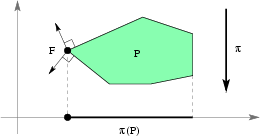 |
| Figure 4: The face F survives the projection |
For fixed d≥2 there are d-dimensional zonotopes with n zones for which a 2-dimensional central section has Ω(nd-1) vertices. For d=2 and d=3 this was known, with 3-dimensional examples provided by the "Ukrainian easter eggs" by Eppstein et al [1]. The result is asymptotically optimal for all fixed d≥2. For a complete proof of this result, more details, and further references see [2].
Zonotopes may be defined as the images of cubes under affine maps, while their duals can be described as the central sections of cross polytopes. So, asking for images of zonotopes under projections, or for central sections of their duals doesn't give anything new: We get again zonotopes, resp. duals of zonotopes. The combinatorics of zonotopes and their duals is well understood: The face lattice of a dual zonotope may be identified with that of a real linear hyperplane arrangement; see Figure 1.
However, surprising effects arise as soon as one asks for
sections of zonotopes, resp. projections of their duals.
Such questions arise in a variety of contexts, such as the examples by Eppstein et al. [1] mentioned above.
It is natural to ask:
What is the maximal number of vertices for a 2-dimensional central
section of a d-dimensional zonotope with n zones?
In the following we consider the dual case.
Using polytope duality and duality between sections and projection we
obtain the following dual formulation of the problem above:
What is the maximal number of vertices for a 2-dimensional projection
(2D-shadow) of a d-dimensional dual zonotope with n zones?
Indeed, the dual question arose independently: It was posed by Vladlen Koltun [3] based on the investigation of his "arrangement method" for linear programming. Our construction shows that the "shadow vertex" pivot rule is exponential in worst-case for the arrangement method.
An upper bound for the maximal size of a 2D-shadow of a dual zonotope is quite obvious: A d-dimensional dual zonotope with n zones has at most two-times n choose d-1 facets all together (it corresponds to a d-dimensional linear hyperplane arrangement, resp. (d-1)-dimensional affine hyperplane arrangement with n hyperplanes; see Figure 1), thus any 2D-shadow has at most O(nd-1) edges resp. vertices.
The lower bound is given by the construction of the dual zonotope Z* presented in the remainder of this article.
Put together, we obtain the following theorem [2]:
For every fixed d≥2 the maximal number of vertices for a 2D-shadow of a
d-dimensional dual zonotope with n zones is Θ(nd-1).
The following construction of Z* is implemented in polymake by the script koltun. Needless to say, polymake also computes the projection to the first two coordinates. Since this construction produces an infinite, two parameter family of polytopes we only include a 3-dimensional example in this eg-model. It is displayed in Figure 1.
For k≥1, n=4k+1, and d≥2 set
b = (k-i)0≤i≤2k = (k,...,-k)T ∈ R2k+1 and
b' = (i-k+1/2)0≤i≤2k-1 = (-k+1/2,...,k-1/2)T ∈ R2k.
Further let 1 and 0 be the "all ones" resp. "all zeroes" vectors of appropriate size and for α=1/(n+1) consider the following matrix A of size (4k+1)(d-1) x d = n(d-1) x d:
b 1 1 0 ... 0 b' -1 1 0 ... 0 α2b 0 α1 α1 ... 0 α2b' 0 -α1 α1 ... 0 ... ... α2(d-2)b 0 0 0 ... αd-21 α2(d-2)b' 0 0 0 ... -αd-21
The matrix A defines a linear hyperplane arrangement A with hyperplanes
Hi = {x ∈ Rd : aix=0} for each row vector ai of A,
and a corresponding dual zonotope
Z* = {x ∈ Rd : Σ1≤i≤n(d-1) |aix| ≤ 1}.
The dual zonotope Z* is d-dimensional and has n(d-1)=O(n) zones.
Via dehomogenization (intersection with the hyperplane x0=1) the linear hyperplane arrangement A yields a (d-1)-dimensional affine hyperplane arrangement, displayed in Figures 2 and 3 for d=2, 3, and 4. Notice the recursive structure of the affine hyperplane arrangements!
Any point x ∈ Rd and hence the cells of A (and also the faces of Z*) have a canonical encoding by sign vectors
sA(x) = (sign a1x, ..., sign an(d-1)x) ∈ {+,0,-}n(d-1).
The matrix A comes with a block structure of d-1 horizontal blocks of size n x d, thus we write the sign vector sA(x) as
sA(x) = (σ1,σ'1; σ2,σ'2; ...; σd-1,σ'd-1) with σi ∈ {+,0,-}2k+1 and σ'i ∈ {+,0,-}2k.
Once the combinatorics of the linear hyperplane arrangement A is understood, that is, once we know the set of sign vectors sA(Rd), we have the following non-redundant facet description of Z*:
Z* = {x ∈ Rd : σAx ≤ 1 for all σ ∈ sA(Rd) corresponding to d-cells of A, i.e. σ has no "0" entries}
A face F of Z* (or in fact of any polytope) survives a projection π if π(F) is equivalent to F and the pre-image of π(F) intersected with Z* is again F. Equivalently, F survives the projection π if and only if the outer normal vectors of the facets containing F, projected to the kernel of π, positively span this kernel; see Figure 4. In the case of π being the projection to the first two coordinates the latter criteria says that for F to survive the outer normals of the facets containing F, truncated to their last d-2 coordinates, must positively span Rd-2.
In [2] it is shown that the 2nd-1+2nd-2 edges corresponding to the following sign vectors (σ1,σ'1; σ2,σ'2; ...; σd-1,σ'd-1) survive the projection to the first two coordinates:
For i=1...d-2 we have (σi,σ'i) = (+...+0-...-,-...-,+...+) or (+...+-...-,-...-0+...+), and the sum over all entries is 0,
and (σd-1,σ'd-1) = (+...+-...-,-...-+...+) with sum 1.
This completes the construction of Z* and the description of the Ω(nd-1) edges which survive the projection to the first two coordinates and thus form the large 2D-shadow. The primal d-zonotope Z is the Minkowski sum of the row vectors of A, that is,
Z = {Σ1≤i≤n(d-1) liai : li ∈ [-1,+1] and ai is the i-th row vector of A}.
The zonotope Z has O(n) zones and its central 2D-section is of size Ω(nd-1).
Model produced with: polymake 2.3
| Keywords | zonotopes; cuts; projections; complexity; Ukrainian easter egg | |
| MSC-2000 Classification | 52B05 (52B11, 52B12, 52C35, 52C40) | |
| Zentralblatt No. | 05613403 |
Submitted: Mon Dec 24 11:31:13 CET 2007.
Revised: Thu Aug 14 09:35:49 CEST 2008.
Accepted: Thu Oct 30 14:18:22 CET 2008.
TU BerlinNikolaus Witte
MA 6-2
10623 Berlin
Germany
thilosch@math.tu-berlin.de
http://www.math.tu-berlin.de/~thilosch
TU BerlinGünter M. Ziegler
MA 6-2
10623 Berlin
Germany
witte@math.tu-berlin.de
http://www.math.tu-berlin.de/~witte
TU Berlin
MA 6-2
10623 Berlin
Germany
ziegler@math.tu-berlin.de
http://www.math.tu-berlin.de/~ziegler