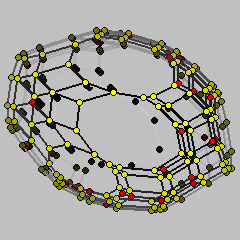
Secondary polytope of a cyclic 8-polytope with 12 vertices

Author

Description

Secondary polytope of an 8-dimensional polytope with 12 vertices which is combintorially equivalent to the cyclic polytope.

The polytope displayed is NOT the secondary polytope of C₈(12) as realized on the standard moment curve (t,t²,...,t⁸). Instead, you see the secondary polytope of the 8-dimensional Carathéodory cyclic polytope with 12 vertices, that is, it is realized on the trigonometric moment curve (sin t, cos t, sin 2t, cos 2t, ..., cos 4t). The secondary of the usual cyclic polytope is too flat to be viewed well. The two types of cyclic polytopes are combinatorially equivalent, but not geometrically. Therefore, the secondary polytopes differ.

The standard realization of the standard C₈(12) has 42(!) non-regular triangulations, all at flip distance 1 from regular ones. They are marked with red vertices. The realization of the Carathéodory cyclic polytope shown has only 38 non-regular triangulations, all of them also at flip distance 1.

The files cyclic* resp. car_cyclic* contain the information about the standard resp. Carathéodory cyclic polytope.

Model produced with: polymake 1.4, TOPCOM 0.9.0

References

1. I.M. Gelfand, M.M. Kapranov, A.V. Zelevinsky: Discriminants, Resultants, and Multidimensional Determinants, Birkhäuser (1994).

Files

• Master File: car_cyclic_8_12.sec.poly
• Applet File: car_cyclic_8_12.sec.jvx
• Preview: car_cyclic_8_12.sec.gif
• Other: car_cyclic_8_12.poly
• Other: car_cyclic_8_12.sec.gml
• Other: car_cyclic_8_12.sec.gml
• Other: cyclic_8_12.poly
• Other: cyclic_8_12.sec.poly
• Other: cyclic_8_12.sec.jvx
• Other: cyclic_8_12.sec.gml

Submission information

Submitted: Sun Sep 10 07:10:24 CET 2000.
Accepted: Mon Nov 20 17:06:57 CET 2000.

Author's Address

Technische Universität Berlin
Fachbereich Mathematik, MA 7-1
Straße des 17. Juni 136
10623 Berlin, Germany
pfeifle@math.tu-berlin.de
http://www.math.tu-berlin.de/~pfeifle