

 |
Hachimori and Ziegler [1] proved that a triangulation of a 3-ball which contains a non-trivial knot consisting of at most 3 edges is not constructible. The following example (constructed along the ideas of Hachimori and Ziegler [1], yet considerably smaller) shows that 3 is the best possible upper bound for the number of edges.
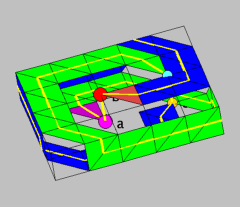
Let C1 be the following triangulation of a pile of 5*4*1 cubes: Each cube is split into 6 tetrahedra, and the tetrahedra are all grouped around one of the diagonal axes of the cube. Furthermore let a denote the pink, b the red, c the orange and d the light blue vertex. For a face F and a vertex x let x*F denote the cone over F with apex x. The pink vertex a and the red vertex b are marked bigger since they are needed for the following: Let C2 := C1 union (a*(green faces)) union (b*(blue faces)), then C2 is a 3-ball with a knot ab-bc-cd-da. Since we add a*(green faces) to C1, the edge da actually exists and adding b*(blue faces) creates the edge bc. The edges ab and cd are already contained in C1. To visualize the knot, one may imagine it as following the yellow line. This knot ab-bc-cd-da is not trivial because ab-bc-cd is a non-trivial knotted spanning arc. It is a shellable 3-ball because C1 is shellable. Note that we do not form the cone over the dark pink face adjacent to a. Similarly we do not form the cone over dark red face adjacent to b.
In order to get a 3-sphere with a knot consisting of 4 edges, one takes the cone over the boundary of C2, that is C := C2 union (v*boundary(C2)), for v not contained in C2. The shelling of C2 can be trivially extended to a shelling of C because boundary(C2) is a 2-sphere and therefore shellable.
Figure 1 depicts the pile of cubes and the faces needed for the construction are colored green and blue. The yellow line visualizes the knot. To obtain the example (shel_3-ball_with_knot.jvx) one has to compleat the construction by adding a*(green faces) and b*(blue faces).
The master file shel_3-ball_with_knot.jvx contains two geometries: The facets of the 3-ball (encoded as their vertex sets) in shelling order and the knot (encoded as the vertex sets of its edges). In the master file point a corresponds to 35, b to 34, c to 15 and d to 14. (If needed, check the applet file for the indices of the other vertices.)
| Keywords | Shellability; Constructibility; Simplicial Ball | |
| MSC-2000 Classification | 52B22 (52B10, 57-99) | |
| Zentralblatt No. | 05264877 |
Submitted: Tue May 8 20:14:13 CEST 2001.
Revised: Fri Jun 14 18:21:37 CEST 2002.
Accepted: Wed Nov 20 15:58:01 CET 2002.
TU Berlin
Fakultät 2, Institut für Mathematik, MA 6-2
Strasse des 17. Juni 136
10623 Berlin, Germany
witte@math.tu-berlin.de