Nonshellable but constructible 2-dimensional simplicial complex

Author

Description

Nonshellable but constructible 2-dimensional simplicial complex

Constructibility is a generalization of shellability defined recursively as: (i) a simplex is constructible, (ii) if C₁ and C₂ are d-dimensional constructible complexes and their intersection is a (d-1)-dimensional constructible complex, then their union is constructible. In this definition, if we restrict C₂ to be a simplex, then the definition becomes equivalent to that of (pure) shellability. Thus constructibility is implied by shellability.

It is known that constructibility is strictly weaker than shellability. For example, Ziegler's nonshellable 3-ball [3] (which is currently the smallest known nonshellable triangulation of a 3-ball) is constructible, and already in [2] it is remarked that other small nonshellable balls (Rudin's example and Gruenbaum's example) are also constructible. On the other hand, in the class of triangulations of 2-dimensional manifolds, it is known that constructibility coincides with shellability. In fact, if a triangulated manifold is constructible then the manifold is a ball or sphere, and any triangulation of a 2-ball and a 2-sphere are shellable.

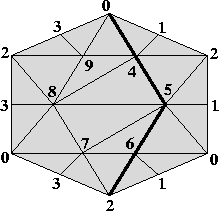
The model we provide here is a 2-dimensional simplicial complex which is nonshellable but constructible. The gif figure is taken from [1]. This figure shows a net of the complex, where the vertices with the same labels should be identified. It is easy to see that this complex is constructible. In fact, if we divide by the bold line, we have two shellable complexes, and their intersection is a shellable 1-complex. On the other hand, this complex is contractible, and it has no boundary. It is known that contractible complexes with no boundaries are nonshellable, see for example [3, p. 84], which assures the nonshellability of our example. In [1] it is shown that a contractible 2-complex is nonconstructible if it has at most one vertex whose link has a cut-vertex. But note that this is not applied to our example because it has two such vertices (0 and 2).

The master file contains a list of facets of this complex together with a suggested coordinatization of vertices in order to realize the model geometrically within 3-dimensional Eucledian space.

Model produced with: Javaview

References

1. M. Hachimori: Decompositions of two-dimensional simplicial complexes (2003), Preprint.
2. J.S. Provan and L.J. Billera: Decompositions of simplicial complexes related to diameters of convex polyhedra, Math. Operations Research 5 (1980), 576-594.
3. R. Stanley: Combinatorics and Commutative Algebra, Second Edition, Birkhauser (1996).
4. G.M. Ziegler: Shelling polyhedral 3-balls and 4-polytopes, Discrete Comput. Geom. 19 (1998), 159-174.

Files

• Master File: nonshel_constr_twodim.jvx
• Applet File: nonshel_constr_twodim.jvx
• Preview: nonshel_constr_twodim.gif

Submission information

Submitted: Fri May 16 12:55:31 CEST 2003.
Revised: Thu Feb 5 04:38:45 CET 2004.
Accepted: Thu Feb 12 16:09:01 CET 2004.

Author's Address

University of Tsukuba
Tsukuba, Ibaraki 305-8573
Japan
hachi@sk.tsukuba.ac.jp
http://www.sk.tsukuba.ac.jp/~hachi/