

 |
 |
 |
 |
We present a vertex-minimal non-shellable simplicial 3-ball and hereby answer a question of Danaraj and Klee [8, p. 40].
The concept of shellability plays an important role in the theory of convex polytopes as well as in topology, combinatorics, and computational geometry; see Ziegler [20] for a survey and further references.
A shelling of a triangulated ball or sphere is a linear ordering of its m facets F_1,...,F_m such that if we remove the facets from the ball or sphere in this order, then at every intermediate step the remaining simplicial complex is a simplicial ball. A simplicial ball or sphere is shellable if it has a shelling; it is extendably shellable if any partial shelling F_1,...,F_i, i<m, can be extended to a shelling. (For a general definition of shellability of simplicial complexes and cell complexes see [3], [20], and [21, Ch. 8].)
Two-dimensional balls and spheres are shellable [2]. The first known example of a non-shellable cellular 3-ball is due to Furch and appeared in 1924 [9]. A non-shellable simplicial 3-ball with 30 vertices and 72 facets was provided by Newman in 1926 [17]. Newman's ball is strongly non-shellable, i.e., it has no free facet that can be removed from the triangulation without loosing ballness.
Much smaller strongly non-shellable simplicial 3-balls were obtained by Grünbaum (cf. [8]) with 14 vertices and 29 facets and by Ziegler [20] with 10 vertices and 21 facets. Rudin's 3-ball [18] with 14 vertices and 41 tetrahedra gives a strongly non-shellable rectilinear triangulation of a tetrahedron with all the vertices on the boundary; the vertices even can be moved slightly to yield a straight triangulation of a convex 3-polytope with 14 vertices [7]. Ziegler's ball is realizable as a straight, yet non-convex ball in 3-space. Coordinates for a rectilinear realization of Grünbaum's ball can be found in [10].
Danaraj and Klee asked in [8, p. 40] ``what is the minimum number of vertices, and of facets, for an unshellable 3-ball''? Triangulated 3-balls with n≤9 vertices were enumerated and tested for shellability in [6]. There is no non-shellable 3-ball with n≤8 vertices, from which it follows that any partial shelling of a 3-ball with n≤8 vertices can be extended to a shelling.
Theorem 1: All triangulated 3-balls with n≤8 vertices are extendably shellable.
Theorem 2: There are precisely twenty-nine vertex-minimal non-shellable simplicial 3-balls with 9 vertices, ten of which are strongly non-shellable. The twenty-nine balls have between 18 and 22 facets, with one unique ball B_3_9_18 having 18 facets and f-vector f=(9,33,43,18).
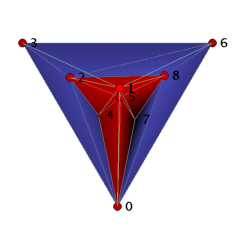
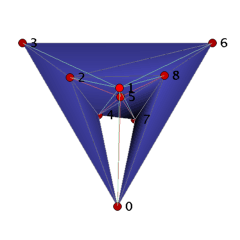
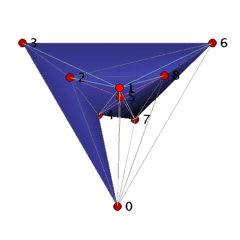
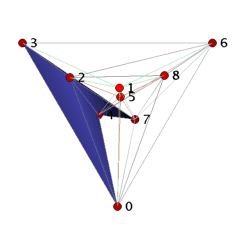
The ball B_3_9_18 can be visualized as a straight, non-convex ball as follows. We start with the facets 0234 and 2347 to which we add in two steps the facets 2367, 2467, 2468 and 4678, 0678. These 7 tetrahedra form a collar for which we close the hole by gluing in 5 triangles 045, 245, 258, 578, and 057. Finally, we place vertex 1 ``above'' the 11 triangles 023, 024, 045, 057, 068, 078, 236, 245, 258, 268, 578, and we add the cone over the triangles with apex 1 to the complex. The 18 tetrahedra together form a 3-ball with one combinatorial symmetry (0,4)(1,2)(3,5)(6,8). It is easy to check that if we remove any tetrahedron, then we loose the ballness.
Conjecture: The ball B_3_9_18 has the smallest number of facets that a non-shellable simplicial 3-ball can have.
If we take the cone over a strongly non-shellable simplicial d-ball with respect to a new vertex, then the resulting simplicial complex is clearly a strongly non-shellable (d+1)-ball with the same number of facets.
Corollary: There are strongly non-shellable simplicial d-balls with d+6 vertices and 18 facets for d≥3.
Klee and Kleinschmidt [13] showed that all simplicial d-balls with up to d+3 vertices are (vertex-decomposable and therefore) shellable. (Not vertex-decomposable d-balls with d+4 vertices, d≥3, are given in [16].) Hence, it remains open whether non-shellable simplicial d-balls with d+4 or d+5 vertices or with fewer than 18 facets exist in dimensions d≥4.
We remark that non-shellable cellular 3-spheres were constructed first by Vince [19] and by Armentrout [1]. Lickorish [14] described non-shellable triangulated 3-spheres that contain a knotted triangle made of the sum of (at least) three trefoil knots; suspensions of such spheres produce non-shellable simplicial PL d-spheres in dimensions d≥4. Hachimori and Ziegler [12] strengthened the result of Lickorish by showing that a triangulated 3-ball or 3-sphere that contains any knotted triangle is (not constructible and thus) non-shellable. An explicit non-shellable triangulated 3-sphere with f-vector f=(381,2309,3856,1928) based on Furch's 3-ball with a knotted spanning arc consisting of one edge was constructed by Hachimori [11]. Examples of non-PL (and hence non-shellable) d-spheres, d≥5, with d+13 vertices can be found in [4]; see also [5]. However, the smallest known non-shellable 3-sphere, constructed by the author [15], has only 13 vertices, f-vector f=(13,69,112,56), and is obtained from a non-constructible 12-vertex 3-ball that contains a trefoil knot consisting of three edges; this sphere gives rise to non-shellable simplicial PL d-spheres with d+10 vertices for d≥3.
| Keywords | shellability; simplicial balls and spheres; constructibility; vertex-decomposability; PL and non-PL triangulations | |
| MSC-2000 Classification | 52B22 (52B05, 57Q15) | |
| Zentralblatt No. | 05264896 |
Submitted: Thu May 29 16:38:08 GMT 2003.
Revised: Tue Mar 16 16:29:57 CET 2004.
Accepted: Sun Mar 21 11:07:26 CET 2004.
Technische Universität Berlin
Fakultät II - Mathematik und Naturwissenschaften
Institut für Mathematik, Sekr. MA 6-2
Straße des 17. Juni 136
10623 Berlin
Germany
lutz@math.tu-berlin.de
http://www.math.tu-berlin.de/~lutz