

 |
 |
We present not vertex-decomposable simplicial d-balls with d+4 vertices for d≥3. Since it is known that d-balls with up to d+3 vertices are vertex-decomposable, these examples are vertex-minimal.
The concept of vertex-decomposability was introduced by Provan and Billera [10] who showed that all vertex-decomposable simplicial complexes, in particular, all vertex-decomposable simplicial spheres, satisfy the (simplicial form of the) famous Hirsch conjecture, which states that the diameter of the dual graph of a pure d-dimensional simplicial complex with n vertices is bounded above by n-(d+1). In fact, the original Hirsch conjecture, formulated by Hirsch in 1957 (cf. [3, p. 168]), plays an important role in the study of the computational complexity of the simplex algorithm of linear programming (see the surveys in [5] and [10]); it asserts that the diameter of the graph of a (d+1)-polytope with n facets, in other words, the number of pivot steps that an edge-following LP algorithm needs for this polytope in the worst case with respect to a best possible choice of the pivots, is smaller or equal to n-(d+1).
A pure d-dimensional simplicial complex K is vertex-decomposable if either K is a simplex (possibly the set containing the empty set) or there is a vertex v such that both the deletion of v in K, i.e., the set del_K(v) of faces of K that do not contain the vertex v, and the link of v in K, i.e., the set link_K(v) of faces of K that do not contain the vertex v, but for which their union with {v} is still in K, are vertex-decomposable pure simplicial complexes.
Provan and Billera [10] proved that triangulated 2-dimensional balls and spheres are vertex-decomposable and thus satisfy the Hirsch conjecture. Klee and Kleinschmidt further showed [5] that all simplicial d-balls (respectively d-spheres) with up to d+3 (respectively d+4) vertices are vertex-decomposable. However, Lockeberg [6] gave a simplicial 4-polytope with 12 vertices whose boundary sphere is not vertex-decomposable, and there even are not vertex-decomposable simplicial 4-polytopes with 10 vertices [5]. The Hirsch conjecture for simplicial spheres was disproved in 1978 by Walkup [11] who provided a 27-dimensional counterexample with 56 vertices. A much smaller counterexample of dimension 11 with 24 vertices is due to Mani and Walkup [9]. Nevertheless, the Hirsch conjecture for (simplicial) d-polytopes is still open for d≥4.
If a simplicial 3-sphere is not vertex-decomposable, then the deletion of any of its vertices yields a not vertex-decomposable simplicial 3-ball. We enumerated in [2] all triangulated 3-spheres (respectively 3-balls) with n≤10 (respectively n≤9) vertices and tested whether they are vertex-decomposable.
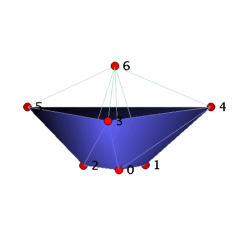
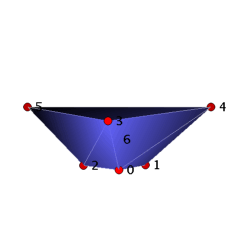
Theorem: There are precisely two vertex-minimal not vertex-decomposable triangulated 3-balls B_3_7_10 and B_3_7_11 with 7 vertices that have 10 and 11 facets, respectively.
It also follows from the enumeration in [2] that all simplicial 3-spheres with n≤8 vertices are vertex-decomposable, but that there are not vertex-decomposable (non-polytopal) simplicial 3-spheres with 9 vertices. The cone over a simplicial d-ball K with respect to a new vertex is a (d+1)-dimensional ball and is vertex-decomposable if and only if K is vertex-decomposable (cf. [10]). A similar statement holds for one-point suspensions of simplicial spheres; see [4].
Corollary: There are vertex-minimal not vertex-decomposable simplicial d-balls with d+4 vertices and 10 facets for d≥3. Moreover, there are not vertex-decomposable simplicial d-spheres with d+6 vertices for d≥3.
This corollary settles, at least for d-balls, a problem of Klee and Kleinschmidt [5, p. 740] who wondered how far the above bounds d+3 and d+4 for d-balls and d-spheres ``can be raised without losing vertex-decomposability''.
The ball B_3_7_10 can be visualized as a straight, convex ball with a Z_3 rotation symmetry as follows. We start with a ring of three tetrahedra 0134, 0235, 1245 and close the hole of the ring by gluing in the triangle 012. Then we place vertex 6 ``above'' the seven triangles 012, 013, 025, 035, 124, 134, 245, and we add the cone over these triangles with apex 6 to the complex. The resulting 3-ball with 7 vertices and 10 facets is not vertex-decomposable, e.g. the deletion of vertex 6 yields the base ring with glued in triangle 012 and hence is not pure. The ball B_3_7_11 can be obtained from B_3_7_10 by adding the tetrahedron 3456, for which vertex 6 has to be placed within the convex hull of the vertices 0-5.
We remark that vertex-decomposable simplicial complexes are shellable. For surveys on shellability, in particular, of balls and spheres, see [1], [12], and [13, Ch. 8]. A vertex-minimal non-shellable 3-ball with 9 vertices and 18 facets is described in [7]. The smallest known non-shellable 3-sphere with 13 vertices and 56 facets can be found in [8].
| Keywords | simplicial balls and spheres; vertex-decomposability; shellability; Hirsch conjecture | |
| MSC-2000 Classification | 52B05 (90C60, 52B22, 57Q15) | |
| Zentralblatt No. | 05264897 |
Submitted: Sun Jun 1 12:11:52 GMT 2003.
Revised: Tue Mar 16 16:29:15 CET 2004.
Accepted: Sun Mar 21 11:07:26 CET 2004.
Technische Universität Berlin
Fakultät II - Mathematik und Naturwissenschaften
Institut für Mathematik, Sekr. MA 6-2
Straße des 17. Juni 136
10623 Berlin
Germany
lutz@math.tu-berlin.de
http://www.math.tu-berlin.de/~lutz