

 |
We present the example of a polyhedral tight immersion of the projective plane with two handles in Euclidean three-space that was introduced by Kühnel and Pinkall in [3].
In the early 1960's Nicolaas Kuiper defined and studied tight immersions of surfaces in Euclidean three-space E3 in [4] and [5].
Let M be a smooth surface with Euler characteristic chi immersed in Euclidean three-space. By definition, the total absolute curvature of M is
tau (M)=intM |K|/2 do,
where K denotes the Gaussian curvature and do is the absolute value of the exterior 2-form which represents the volume. With Gauss-Bonnet's theorem and the knowledge of the following inequality for the integral over all points of positive Gaussian curvature K
intK>0 K/2\pi do ≥ 2,
it follows that the following inequality holds for immersions of closed surfaces in Euclidean three-space
tau (M)=intM |K|/2 pi do ≥ 4-chi(M).
If equality occurs here, the immersion f: M to E3 is called tight, which means that the surface has minimal total absolute curvature. Tightness is a generalization of the notion of convexity. In some sense, it means that a surface is embedded or immersed 'as convexly as possible' with respect to its topological properties. With the introduction of the two-piece-property (TPP), which is equivalent to equality in the above inequality, for surfaces in E3 it was possible to examine tightness not only for smooth surfaces but also for polyhedral ones as it was done by Banchoff in [1]. For all surfaces --- smooth or polyhedral --- it is known whether they can be immersed or embedded tightly in three-space or not. A good collection of the known results and a huge reference list on tightness can be found in [2].
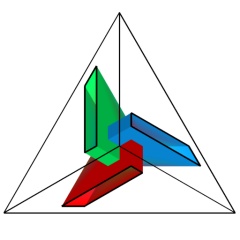
It was Kuiper in [5] who stated that there exists a (smooth) tight immersion of the tight projective plane with two handles in Euclidean three-space. There can also be found a very complicated construction of this immersion. It seems to be very difficult to prove rigorously that the described surface is tight although we have no doubt that the idea behind this construction is essentially correct. In this sense the example introduced in [3] and presented here, a polyhedral tight immersion of the projective plane with two handles in Euclidean three-space, was a great improvement. It was explicitely given and the tightness can be seen very easily (all the strict local supporting planes of the presented polyhedral Boy surface with two handles concentrate at the vertices of the tetrahedron which implies the tightness of the surface). Moreover the given polyhedral immersion is tightly smoothable with the algorithm given and proved in the cited paper [3] (all of the vertices are of valence three therefore the algorithm is applicable) which means that the surface can be smoothed while preserving tightness and the topological properties which proves the mentioned theorem by Kuiper more easily. Additionally the presented surface has a three-fold symmetry.
Every vertex lies in the cubic lattice Z3 < E3 where the origin is the triple point of the Boy surface which is not a point of the surface. The vertices are given as follows where the three-fold symmetry appears as a cyclic shift of the three coordinates (x to y to z to x) corresponding to the cyclic shift of the indices (1 to 2 to 3 to 1) of the presented vertices:
A1=(-1,1,0) A2=(0,-1,1) A3=(1,0,-1) B1=(-1,1,-1) B2=(-1,-1,1) B3=(1,-1,-1) C1=(-1,0,-1) C2=(-1,-1,0) C3=(0,-1,-1) D1=(0,2,1) D2=(1,0,2) D3=(2,1,0) E1=(-1,2,1) E2=(1,-1,2) E3=(2,1,-1) F1=(-1,0,-2) F2=(-2,-1,0) F3=(0,-2,-1) G1=(-4,-1,2) G2=(2,-4,-1) G3=(-1,2,-4) H1=(-5,0,2) H2=(2,-5,0) H3=(0,2,-5) J1=(2,2,-8) J2=(-8,2,2) J3=(2,-8,2) K=(2,2,2)
The vertices J1, J2, J3 and K span the tetrahedron which contains a polyhedral Boy surface spanned by the 24 vertices Ai, Bi, ..., Hi, i=1,2,3. The 13 faces of this Boy surface split into 5 different types under the three-fold symmetry:
type 1: (E1, G3, F1, C1, B1, A1, C2, B2),
type 2: (A2, C3, F3, H3, D1),
type 3: (B2, A2, D1, E1),
type 4: (E1, D1, H3, G3),
type 5: (H2, F2, G1, H1, F1, G3, H3, F3, G2).
These faces lie in different planes, namely x=-1, x=0, z=1, y=2 and x+y+z=3, and intersect in a curve which is a closed space polygon and given by the following points:
(O L1 N2 M2 O L2 N3 M3 O L3 N1 M1 O),
which are defined as:
L1=(1,0,0) L2=(0,1,0) L3=(0,0,1) M1=(-1,0,0) M2=(0,-1,0) M3=(0,0,-1) N1=(-1,0,1) N2=(1,-1,0) N3=(0,1,-1) O=(0,0,0).
The presented geometry is built up of the faces given above with the given coordinates.
The Euler-characteristic chi of the Boy surface is easily computed to be chi=24-36+13=1. After gluing it together with the tetrahedron in the way as it can be seen in the model (the faces of type 4 indicate the way, the tetrahedron and the Boy surface are glued together) we get chi=28-42+11=-3. Note that the faces of the tetrahedron are not contractible, with the result that they do not make a contribution to the Euler-characteristic. Therefore the shown surface is a polyhedral tight immersion of the projective plane with two handles as stated.
Model produced with: JavaView v.2.21
| Keywords | Tight surface; Total absolute curvature; Projective plane; Euclidean 3-space | |
| MSC-2000 Classification | 53C42 | |
| Zentralblatt No. | 05264894 |
Submitted: Wed May 14 14:50:05 GMT 2003.
Revised: Fri Aug 20 10:10:50 CEST 2004.
Accepted: Sat Sep 4 11:13:43 GMT 2004.
University StuttgartMarc-Oliver Otto
Department of mathematics
Institute of geometry and topology
Pfaffenwaldring 57
70550 Stuttgart
Germany
Bulach@mathematik.uni-stuttgart.de
http://www.mathematik.uni-stuttgart.de/igt/LstGeo/Bulach/
University Stuttgart
Department of mathematics
Institute of geometry and topology
Pfaffenwaldring 57
70550 Stuttgart
Germany
Otto@mathematik.uni-stuttgart.de
http://www.mathematik.uni-stuttgart.de/igt/LstDiffgeo/Otto/