A counterexample to A.D. Alexandrov's conjecture

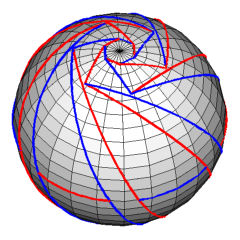
Figure 1: The graph G

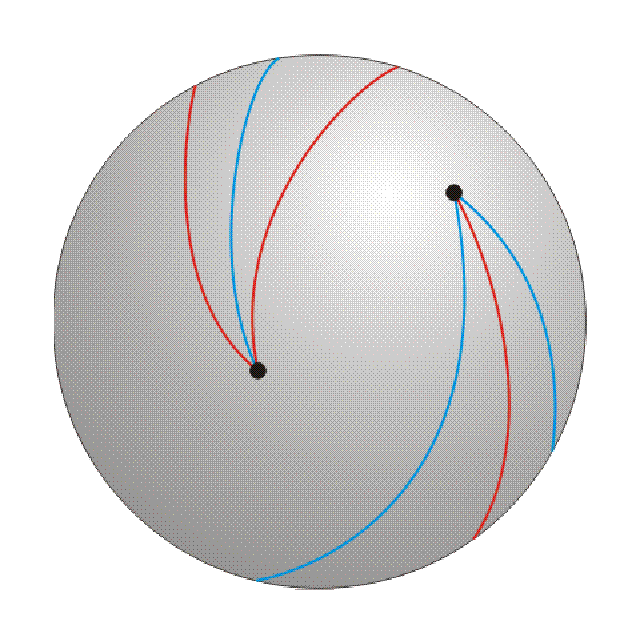Figure 2: Two local colorings

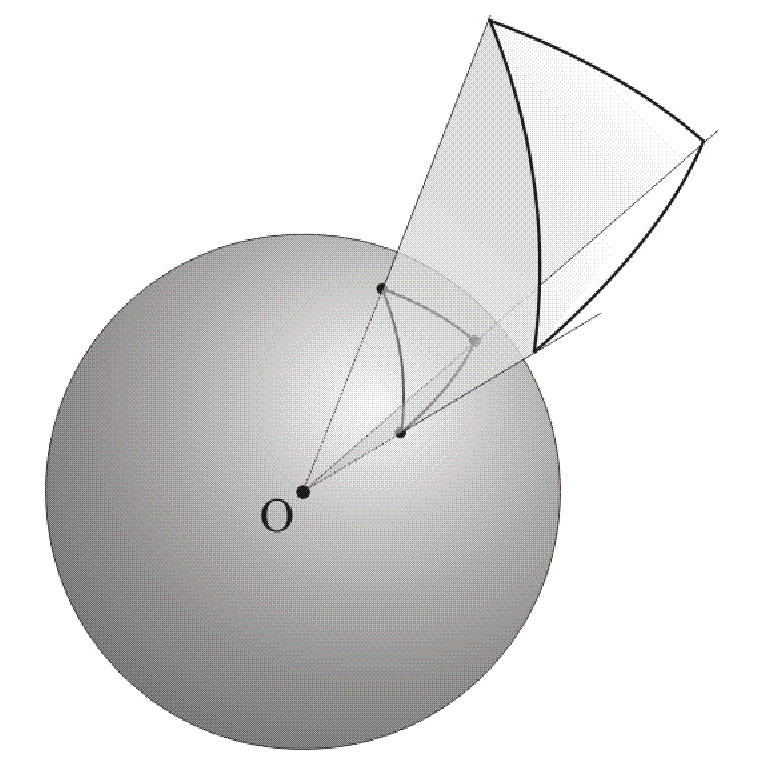Figure 3

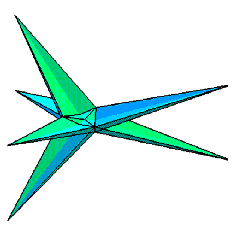Figure 4: Hyperbolic virtual polytope

Authors

Description

A pointed graph on the sphere which leads to a counterexample to A.D. Alexandrov's conjecture.

We present a graph G embedded in the sphere S² such that:

• Its edges are non-crossing geodesic segments shorter than pi.
• The graph is trivalent (each vertex has exactly 3 incident edges).
• The embedding is pointed (each vertex has an incident angle larger than pi).
• Finally, the edges are colored red and blue. At each vertex, only two types of coloring are allowed (Fig. 2).

It is pretty difficult to find such an example (try by yourself!), but still there are many of them.

This graph is interesting and important not only because of its funny combinatorics, but also because it leads to a counterexample to A.D. Alexandrov's uniqueness conjecture for smooth convex surfaces:

Let K in R³ be a smooth closed convex surface. If a constant C separates non-strictly principal curvature radii at every point of the boundary of K, then K is a ball.

This was proven by A.D. Alexandrov in [1] for analytic surfaces; however, the general case ( for smooth surfaces) stood open for a long time. The first counterexample by Y. Martinez-Maure appeared in 2001.

We explain below how the graph G leads to a counterexample to the conjecture, referring the reader to [2-5] for details.

• The graph G generates a tiling of the sphere. Each tile spans a cone. Thus, the graph G generates a conical tiling T(G) of the space R³ (Fig. 3).
• Lifting up. The tiling T(G) possesses the following property: there exists a continuous piecewise linear (but not globally linear!) function h :R³ --> R which is linear on each of the cones. The function h is called the lifting of the graph G. For this particular example, the lifting is unique up to a scale.
• The existence of a lifting is a non-trivial property of the graph G. It should be mentioned that no pointed graph in the plane has a lifting.
• The function h is saddle. That is, for each plane e, the graph of the restriction of the function h on the plane e is a saddle surface (it is a consequence of the pointed property).
• The function h can be smoothened. Namely, there exists a smooth function h' which approximates h, and which is saddle in the sense of (3).
• We add next a large ball. Namely, let h" be the support function of a ball which is sufficiently large to make the sum h'+h" convex. Then h'+h" is the support function of some convex body K. It is a counterexample to the conjecture. Enjoy!

This example illustrates a small part of the theory of hyperbolic virtual polytopes .

The below brief explanation contains no precise definitions and constructions, for which we refer the reader to [2,4,5]. Virtual polytopes are Minkowski differences of convex polytopes. They can be introduced as just formal expressions, but the key point is that the formal differences can be interpreted geometrically. Basic geometric notions for convex polytopes (such as volume, faces, outer normal fan, etc.) can be extended to virtual polytopes. In particular, it makes sense to speak of the support function of a virtual polytope.

When passing from convex polytopes to virtual polytopes, we loose convexity. Generically, a virtual polytope has a mixed type of convexity: it has a convex part (whatever this means), a concave part, and a saddle part. Virtual polytopes whose support function is saddle are called hyperbolic.

From this viewpoint, the above example presents the support function h of some hyperbolic virtual polytope K. The geometric interpretation of the virtual polytope K is is a polyhedral self-intersecting surface (Fig. 4). By construction, the graph G plays the role of the normal fan of K.

Model produced with: Maple 7 + JavaViewLib 3.95.000

References

1. A.D. Alexandrov: On uniqueness theorems for closed surfaces (Russian), Doklady Akad. Nauk SSSR 22 (1939), 99--102, .
2. M. Knyazeva, G. Panina: An illustrated theory of hyperbolic virtual polytopes, CESJM, to appear (2008), .
3. Y. Martinez-Maure: Contre-exemple \`a une caract\'erisation conjectur\'ee de la sph\`ere, C.R. Acad. Sci., Paris 332 (2001), 41--44, .
4. G. Panina: New counterexamples to A.D. Alexandrov's uniqueness hypothesis, Advances in Geometry 5 (2005), 301--317.

Files

• Master File: KP.jvx
• Master File: KP4.jvx
• Applet File: KP.jvx
• Applet File: KP4.jvx
• Preview: KP1.jpg
• Preview: KP4.gif
• Image: KP2.gif
• Image: KP3.gif

240x240 preview

Submission information

Submitted: Thu Apr 17 10:06:36 CEST 2008.
Revised: Fri Mar 20 14:05:24 CET 2009, Tue Apr 21 10:05:42 CEST 2009, Thu May 7 11:21:58 CEST 2009.
Accepted: Thu Feb 18 12:13:46 CET 2010.

Authors' Addresses

Saint-Petersburg Institute for Informatics and Automation RAS
14 line V.O., 39
Saint-Petersburg
Russia
marinakn@mail.ru

Saint-Petersburg Institute for Informatics and Automation RAS
14 line V.O., 39
Saint-Petersburg
Russia
gaiane-panina@rambler.ru
http://club.pdmi.ras.ru/~panina