

 |
 |
 |
 |
 |
 |
 |
 |
Using Hilbert's definition of a heptahedron we show how to construct Steiner's Roman surface as a model of the projective plane. It is well known that both surfaces are topological models of the projective plane [2].
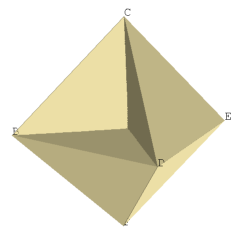
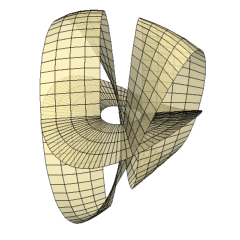
The heptahedron consists of six vertices with (x, y, z) coordinates A(1,0,0), B(0,1,0), C(0,0,1), D(-1,0,0), E(0,-1,0), F(0,0,-1), twelve edges AB, BD, DE, EA, AC, BC, DC, EC, AF, BF, DF, EF and seven faces ABC, CDE, AEF, BDF, BCEF, ACDF, ABDE as shown in Figure I. The three square faces intersect in three mutually perpendicular straight line segments that are not edges and a point in the center that is not a vertex. Exactly two faces meet at every edge and we can travel from any face to any other face by crossing edges. The result is a polyhedron called the heptahedron which was originally constructed by David Hilbert [1].
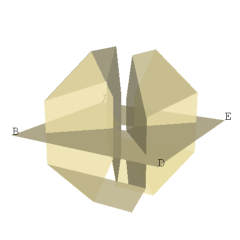
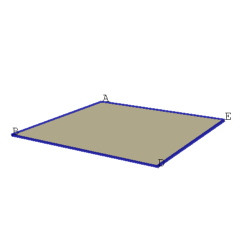
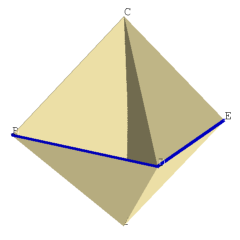
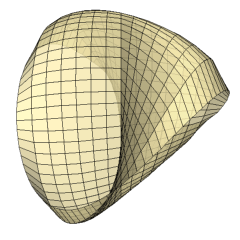
We shall first show that the heptahedron is topologically equivalent to a Möbius band joined along its boundary to the boundary of a disc. To visualize this, we cut a small portion of the surface along the z-axis and along the edges of the square face ABDE above and below the xy-plane as shown in Figure II. A simple band without any twists and a disc with a hole are now visible in Figure II. Closing the hole of the disc recovers the square face ABDE, shown in Figure III. Rejoining the simple band along the inside portion of its boundary yields a Möbius band, shown in Figure IV. If we now rejoin the boundary of the disc along the edge of the Möbius band, we can recover the original heptahedron of Figure I.
Next, referring to Figure II, we deform the simple band in the Heptahedron to the simple band given by Equation I:
z=(xy/(2x2+2y2))(-1-(1-4x2-4y2)1/2)
for epsilon≤x2+y2≤1/4-epsilon and we deform the disc with the hole in the heptahedron to the disc with a hole given by Equation II:
z=(xy/(2x2+2y2))(-1+(1-4x2-4y2)1/2)
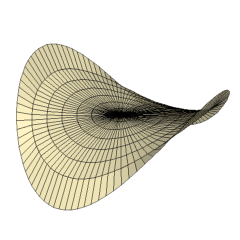
for epsilon≤x2+y2≤1/4-epsilon where epsilon>0 is a small constant. The result is shown in Figure V. Now let epsilon approach zero in Figure V. We obtain a disc given by Equation II for 0≤x2+y2≤1/4 shown in Figure VI. We also obtain a Möbius band given by Equation I for 0≤x2+y2≤1/4 shown in Figure VII.
Finally, to complete the deformation, the boundaries of the Möbius band and disc are joined along the curve given by z=2xy for x and y on the circle x2+y2=1/4. The resulting closed surface shown in Figure VIII is called the Roman surface which was first discovered by Jakob Steiner.
The equation for the Roman surface may be obtained as follows. For any fixed x and y, Equation I and Equation II are roots of the quadratic equation in z given by Equation III:
(x2+y2)z2+(xy)z+(x2y2)=0.
Thus from Equation III, the Roman surface is a surface of the fourth order given by Equation IV:
x2y2+x2z2+y2z2+xyz=0.
Note that all surfaces given by the equation
x2y2+x2z2+y2z2+2kxyz=0
where k is nonzero, are called Roman surfaces. We have used k=1/2 to make the above argument.
The heptahedron and Roman surface are both nonorientable surfaces since they contain a Möbius band. Being equivalent to a Möbius band joined along its boundary to the boundary of a disc, both the heptahedron and Roman surface are topological models of the projective plane.
Model produced with: JavaView v.2.21
| Keywords | Heptahedron; Roman surface; Projective plane; Möbius band | |
| MSC-2000 Classification | 57M20 (57N35) | |
| Zentralblatt No. | 05264893 |
Submitted: Wed May 14 13:15:04 GMT 2003.
Revised: Thu Jul 22 14:06:03 CEST 2004.
Accepted: Sat Sep 4 11:38:18 GMT 2004.
Ansal Institute of Technology
H-501 Palam Vihar
District Gurgaon
Haryana 122017
India
ashay@dharwadker.org
http://www.dharwadker.org/