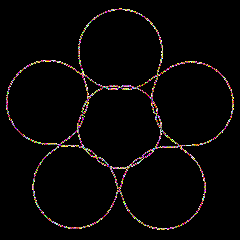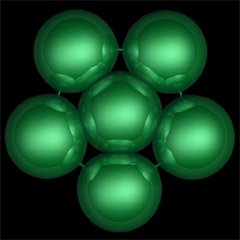
Penta - A Constant Mean Curvature Surface of Genus 5

Authors

Description

Penta is an experimentally found compact constant mean curvature surface with low genus.

We have performed numerical experiments that suggest the existence of compact constant mean curvature surfaces with low genus [1]. Our surfaces come in three dihedrally symmetric families with the genus ranging from 3 to 5, 7 to 10, and 3 to 9, respectively; there are further surfaces with the symmetry of the Platonic polyhedra and genera 6, 12, and 30. We use the algorithm of Oberknapp and Polthier [10] that defines computes discrete constant mean curvature with a discrete version of Lawson's conjugate surface method. The Penta surface is an example of this family with genus 5.

Surfaces with constant mean curvature H have been studied for a long time. Until recently most known boundaryless or complete surfaces were minimal (H = 0); the only surfaces with non-zero constant H were Delaunay's surfaces of revolution [4]. Compact surfaces have attracted particular attention. Whereas the maximum principle rules out the existence of compact minimal surfaces, some constructions for H > 0 are known by now [12][7]. Often, the resulting compact surfaces are rather complicated and also not quite as explicit as one might hope. The Penta surface [5] is an example of a compact surfaces which is geometrically simpler and has a large symmetry group.

Let us assume H is a nonzero constant and normalize it to 1 by a scaling; we use the shorthand notation cmc for this case. The simplest compact cmc surface is the unit sphere. The sphere is known as the unique embedded cmc surface [2], and also the unique immersed cmc sphere [6]. Both results focused much attention on the existence problem for further compact cmc surfaces. It is also interesting that the sphere is the only complete cmc surface which is a minimum for the variational problem for constant mean curvature [13]: find critical levels of area for a given enclosed volume. The partial differential equation H = const. can be considered the Euler equation to the variational problem.

Wente's existence proof for cmc tori [12] was a surprising event which triggered further discoveries. Pinkall and Sterling [11] characterize all immersions that cover cmc tori, and Bobenko [3] gives explicit formulae for their induced metrics in terms of theta functions. These immersions lead to compact cmc tori only if all periods vanish, otherwise to non-compact periodic surfaces.

Kapouleas [7] constructs a large class of compact cmc surfaces for every genus g > 3. Kapouleas glues pieces of Delaunay surfaces onto spheres and proves existence of nearby smooth cmc surfaces by an implicit function theorem argument. The Delaunay pieces must be long, and all necksizes tiny - how long and how thin precisely is the result of delicate estimates and hence practically not accessible. In [14] surfaces of every genus g > 2 are constructed using g Wente tori that are glued together at a single lobe. Similar to the case of Kapouleas' Delaunay-like surfaces the fused Wente tori are almost degenerate: they have a large number of almost spherical lobes joined by necks of large Gauß curvature.

Lawson's [9] conjugate surface method generates symmetric surfaces by planar reflection from a simply connected fundamental domain. For all our surfaces this domain is bounded by five planar arcs and depends on two parameters. On the other hand there are two period conditions to satisfy. To solve these two period problems rigorously is a serious problem for our domains (see ), and this is the main reason why we must rely on a numerical method.

Model produced with: Grape; JavaView 1.99.9

References

1. Karsten Grosse-Brauckmann and Konrad Polthier: Compact Constant Mean Curvature Surfaces with Low Genus, Experimental Mathematics 6, 1 (1997), 13--32.
2. A.D. Alexandrov: Uniqueness theorems for surfaces in the large. V, Amer. Math. Soc. Transl. 21, 2 (1962), 412--416.
3. A.I. Bobenko: All constant mean curvature tori in R3, S3, H3 in terms of theta functions, Math. Ann. 290, 2 (1991), 209--245.
4. C. Delaunay: Sur la surface de revolution, dont la courbure moyenne est constante, Journal de mathematiques 6 (1841), 309--320.
5. K. Grosse-Brauckmann and K. Polthier: Numerical examples of compact constant mean curvature surfaces, in B. Chow and R. Gulliver and S. Levy and J. Sullivan (Eds.): Elliptic and parabolic methods in geometry, A K Peters, Wellesley (1996), 23--46.
6. H. Hopf: Differential geometry in the large, 2nd ed., Lecture Notes in Mathematics 1000, Springer 1989 (1956).
7. N. Kapouleas: Compact constant mean curvature surfaces in Euclidean three-space, J. Diff. Geom. 33, 3 (1991), 683--715.
8. N. Korevaar, R. Kusner, W.H. Meeks, B. Solomon: Constant mean curvature surfaces in hyperbolic space, Am. J. Math. 114, 1 (1992), 1--43.
9. H.B. Lawson: Complete minimal surfaces in S3, Ann. of Math 92, 2 (1970), 335--374.
10. B. Oberknapp and K. Polthier: An algorithm for discrete constant mean curvature surfaces, in H.-C. Hege and K. Polthier (Eds.): Visualization and Mathematics, Springer Heidelberg (1997), 141--161.
11. U. Pinkall and I. Sterling: On the classification of constant mean curvature tori, Ann. of Math. 130, 2 (1989), 407--451.
12. H. Wente: Counterexample to a conjecture of H. Hopf, Pac. J. of Math 121, 1 (1986), 193--243.
13. J.L. Barbosa and M. do Carmo: Stability of hypersurfaces with constant mean curvature, Math. Z. 185 (1984), 339--353.
14. N. Kapouleas: Constant mean curvature surfaces by fusing Wente tori, Invent. Math. 119, 3 (1995), 443--518.

Files

• Master File: Penta_Master.jvx
• Applet File: Penta_Applet.jvx
• Preview: Penta_Preview.jpg
• Preview: Penta_Equator.gif
• Other: Penta_Fundamental.jvx
• Other: Penta_10000.byu

Penta_Master: Geometry with full resolution. Penta_Applet: Geometry with resolution reduced to 2000 triangles. Penta_Fundamental: Fundamental domain for symmetry group, can be used to generate the master geometry. Penta_Equator: image of a horizontal symmetry line Penta_10000: Geometry with resolution reduced to 10000 triangles.

Submission information

Submitted: Sun Sep 10 07:10:24 CET 2000.
Accepted: Mon Nov 20 17:06:57 CET 2000.

Authors' Addresses

Universität Bonn
Beringstr. 1
53123 Bonn
kgb@math.uni-bonn.de
http://www.math.uni-bonn.de/people/kgb/

Universitätsbibliothek Freiburg
Werthmannplatz 2
79098 Freiburg
bo@ub.uni-freiburg.de

Technische Universität Berlin
Fachbereich 3 Mathematik
Strasse des 17. Juni 136
10623 Berlin
polthier@math.tu-berlin.de
http://www-sfb288.math.tu-berlin.de/~konrad/