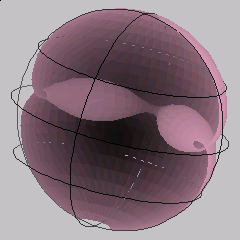Mean Curvature 1 Warped Catenoid Cousins in Hyperbolic 3-Space

Authors

Description

These three surfaces are mean curvature 1 surfaces in hyperbolic 3-space. They each have two regular embedded ends, but are not surfaces of revolution. Only one of two congruent pieces of each surface is shown. (Hyperbolic 3-space is shown here using the Poincare model.)

Robert Bryant, in [1], found a representation for mean curvature 1 surfaces in hyperbolic 3-space. This representation is similar to the Weierstrass representation for minimal surfaces in Euclidean 3-space, in that it also produces surfaces from a meromorphic function and a holomorphic 1-form on a Riemann surface.

Using this representation, Bryant explicitly described all mean curvature 1 surfaces of revolution, which he called catenoid cousins. See the model entitled "Mean curvature 1 surfaces of revolution in hyperbolic 3-space" in this model server, by the same authors.

In the work [4], this representation was used to find many other examples, including the examples shown here. In [4] all mean curvature 1 genus 0 surfaces in hyperbolic space with two regular ends were classified (the definition of a regular end is also found in [4]). This classification includes surfaces whose ends are not embedded, but we only show examples with embedded ends here, as these are the ones that are most easily understood visually. We call the surfaces in this classification "warped catenoid cousins".

These example are particularly interesting in that they show how mean curvature 1 surfaces in hyperbolic 3-space can have different properties from minimal surfaces in Euclidean 3-space, even though they have such similar meromorphic representations. Richard Schoen, in [2], showed that any complete connected finite-total-curvature minimal immersion into Euclidean 3-space with two embedded ends is a catenoid. The examples here show that the corresponding property for mean curvature 1 surfaces in hyperbolic 3-space does not hold.

The classification of warped catenoid cousins was refined into a more explicit form in the work [3].

A more detailed description of these surfaces can be found in the LaTeX, postscript, pdf and Mathematica files included in this model.

Model produced with: JavaView v.2.00.a2

References

1. Robert Bryant: Surfaces of mean curvature one in hyperbolic space, Asterisque 154-155 (1987), 321--347.
2. Richard Schoen: Uniqueness, symmetry, and embeddedness of minimal surfaces, J. Differential Geometry 18 (1982), 791--809.
3. Wayne Rossman and Masaaki Umehara and Kotaro Yamada: Mean curvature 1 surfaces in hyperbolic 3-space with low total curvature II, preprint (2000).
4. Masaaki Umehara and Kotaro Yamada: Complete surfaces of constant mean curvature-1 in the hyperbolic 3-space, Annals of Mathematics 137 (1993), 611--638.

Files

• Master File: warpedcatenoidcousin1_Master.jvx
• Master File: warpedcatenoidcousin2_Master.jvx
• Master File: warpedcatenoidcousin3_Master.jvx
• Applet File: warpedcatenoidcousin1_Applet.jvx
• Applet File: warpedcatenoidcousin2_Applet.jvx
• Applet File: warpedcatenoidcousin3_Applet.jvx
• Preview: warpedcatenoidcousin1_Preview.gif
• Preview: warpedcatenoidcousin2_Preview.gif
• Preview: warpedcatenoidcousin3_Preview.gif
• Other: warpedcatenoidcousins.nb
• Other: CMC1surfaces.tex
• Other: CMC1surfaces.ps
• Other: CMC1surfaces.pdf

Submission information

Submitted: Tue Jan 23 17:56:59 CET 2001.
Revised: Tue Feb 12 09:26:59 CET 2002.
Accepted: Wed Feb 20 12:44:06 CET 2002.

Authors' Addresses

Kobe University
Mathematics Department
Faculty of Science
Rokko, Kobe 657-8501
Japan
wayne@math.kobe-u.ac.jp
http://www.math.kobe-u.ac.jp/HOME/wayne/wayne.html

Hiroshima University
Mathematics Department
Faculty of Science
Higashi-Hiroshima 739-8526
Japan
umehara@math.sci.hiroshima-u.ac.jp
http://www.math.sci.hiroshima-u.ac.jp/~umehara/

Kyushu University 36, 6-10-1
Faculty of Mathematics
Hakozaki, Higashi-ku, Fukuoka 812-8185
Japan
kotaro@math.kyushu-u.ac.jp
http://www.math.kyushu-u.ac.jp/kotaro/