CMC cylinder - Bäcklund transform of a perturbed Delaunay unduloid

Authors

Description

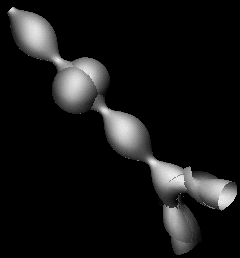
This CMC cylinder is a Bäcklund transform of a perturbed Delaunay unduloid.

Smooth surfaces of constant mean curvature in Euclidean three space are characterized by the fact that their Gauss map is harmonic. Such harmonic maps can be obtained by a Weierstrass Type Representation [2], commonly referred to as the DPW method, that naturally incorporates dressing [1] as a means of perturbing the harmonic map. The classical Bäcklund transformation corresponds to dressing by 'simple factors' and adds bubbles to the surface [7], [8].

A family of surfaces similar to this model are discussed in detail in [4] as pertubations of Delaunay surfaces: The idea is to take a DPW potential of a Delaunay unduloid - a holomorphic loop valued 1-form on the twice punctured Riemann sphere with simple poles at the origin and the point at infinity and perturb it, by adding an entire term, to change the geometry of the end at infinity. The initial condition in the DPW method then needs to be computed numerically to ensure that the resulting surface again closes [4]. Such surfaces look like our model, but without the bubbles. They may have an arbitrary number of umbilic points and have one Delaunay end. The other highly self intersecting end resembles that of a Smyth surface [6].

The novelty of this model is that by choosing an appropriate simple factor, it is possible to add bubbles onto the surface: This is possible since the perturbed surface still has Delaunay monodromy, which is known explicitly [3] and thus allows the choice of singularity in the simple factor to attain any value where the monodromy is reducible. For a recent account of these techniques we refer to [5].

Model produced with: GANGLab 1.0, Nicholas Schmitt

References

1. F. E. Burstall and F. J. Pedit: Dressing orbits of harmonic maps, Duke Math. J. 80 (1995), 353-382, .
2. J. Dorfmeister and F. Pedit and H. Wu: Weierstrass type representation of harmonic maps into symmetric spaces, Com. Anal. Geom. 6 (1998), 633-667, .
3. M. Kilian: Constant mean curvature cylinders (2000), Ph.D. thesis, Univ. of Massachusetts, .
4. M. Kilian, I. McIntosh and N. Schmitt: New constant mean curvature surfaces, Experiment. Math. 9:4 (2000), 595--611, .
5. M. Kilian, N. Schmitt and I. Sterling: Dressing CMC n-Noids, Math. Z. 246 (2004), 501--519, .
6. B. Smyth: A generalization of a theorem of Delaunay on constant mean curvature surfaces, IMA Vol. Math. Appl. 51 (1993), 123-130, .
7. I. Sterling and H. Wente: Existence and classification of constant mean curvature multibubbletons of finite and infinite type, Indiana Univ. Math. J. 42 (1993), 1239-1266, .
8. C. Terng and K. Uhlenbeck: Backlund transformations and loop group actions, Comm. Pure and Appl. Math LIII (2000), 1-75, .

Files

• Master File: cmccyl_Master.jvx
• Applet File: cmccyl_Applet.jvx
• Preview: cmccyl_Preview.gif

Submission information

Submitted: Wed Dec 12 23:52:28 GMT 2001.
Revised: Thu Jul 22 13:50:36 CEST 2004.
Accepted: Sat Sep 4 11:32:21 GMT 2004.

Authors' Addresses

Amherst College
Amherst, MA 01002
kilian@gang.umass.edu
http://www.gang.umass.edu/~kilian

University of Massachusetts
Amherst, MA 01002
nick@math.umass.edu
http://www.gang.umass.edu/~nick