Discrete bubbletons in Euclidean 3-space

Authors

Description

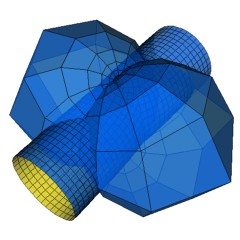
The depicted net is a cmc Darboux transform of a discrete cylinder.

The model is a discrete bubbleton, which is a discrete constant mean curvature surface obtained from a (discrete) cylinder by a Darboux or Bianchi-Baecklund transformation, cf. [8].

A smooth constant mean curvature surface in Euclidean 3-space has (away from umbilics) a parallel constant mean curvature surface (Bonnet's theorem). On the one hand, this parallel surface carries a conformally equivalent metric, has corresponding curvature directions and also parallel tangent planes and, therefore, is a Christoffel transform of the original surface. On the other hand, besides carrying a conformally equivalent metric and corresponding curvature directions, it is the second envelope of a 2-parameter family of spheres (of constant radius) and, therefore, it is also a Darboux transform of the original surface. It turns out that these facts provide a characterization for surfaces of constant mean curvature among all isothermic surfaces [5].

Half way between two parallel cmc surfaces there is a (possibly degenerate) surface of constant (positive) Gauss curvature. For such surfaces, Bianchi defined a Baecklund transformation [1] which can be arranged, by aligning parameters appropriately, to provide a real surface after two transformations, see [10]. This provides a notion of Bianchi-Baecklund transformation for surfaces of constant mean curvature. The smooth (single-) bubbletons are obtained by this procedure from the cylinder: they are parallel to Sievert's surfaces [9], see [10] and [8]. Multiple application of the transformation provides the multibubbletons of [10].

On the other hand, the Darboux transformation transforms cmc surfaces (considered as isothermic surfaces) to cmc surfaces when the involved parameters are chosen appropriately, cf. [2]. It turns out that these Darboux transformations are the aforementioned Bianchi-Baecklund transformations, see [5] and [8], so that (single- and multi-) bubbletons can be obtained by (one resp. mutliple) Darboux transformations from a cylinder.

Using the transformation theory for discrete isothermic nets then yields a definition for discrete cmc nets by requiring the existence of a simultaneous Christoffel and Darboux transform of an isothermic net, see [6]. These discrete cmc nets can as well be defined in an analytic way by discretizing the frame equations, which yields a unit normal field that is defined on the vertices of the net and provides another way of defining the parallel surface, see [3]. Note that this definition can be extended to discrete isothermic nets in the broad sense, that is, for discrete nets with factorizing cross ratios rather than just cross ratio -1, cf. [7].

Also, by using the appropriate Bianchi permutability theorems, one can show that discrete cmc nets in this sense allow a (1+2)-parameter family of Darboux transformations into discrete cmc nets, see [6]. The described model is obtained as such a Darboux transform of a discrete cylinder.

Model produced with: Mathematica and JavaView v3.00

References

1. L. Bianchi: Vorlesungen ueber Differentialgeometrie, Teubner, Berlin (1899), .
2. L. Bianchi: Ricerche sulle superficie isoterme e sulla deformazione delle quadriche, Ann. Mat. 11 (1905), 93-157, .
3. A. Bobenko, U. Pinkall: Discretization of surfaces and integrable systems, in A. Bobenko, R. Seiler (Eds.): Discrete integrable geometry and physics, Clarendon Press, Oxford (1999), 3-58, .
4. G. Darboux: Sur les surfaces isothermiques, Comptes Rendus 128 (1899), 1299-1305, 1538, .
5. U. Hertrich-Jeromin, F. Pedit: Remarks on the Darboux transform of isothermic surfaces, Doc. Math. J. DMV 2 (1997), 313-333, .
6. U. Hertrich-Jeromin, T. Hoffmann, U. Pinkall: A discrete version of the Darboux transform for isothermic surfaces, in A. Bobenko, R. Seiler (Eds.): Discrete integrable geometry and physics, Clarendon Press, Oxford (1999), 59-81, .
7. U. Hertrich-Jeromin: Introduction to Moebius differential geometry, Cambridge Univ. Press (2003), .
8. S. Kobayashi: Bubbletons and their parallel surfaces in Euclidean 3-space (2002), Electronic Geometry Model No. 2002.03.001, http://www.eg-models.de/2002.03.001.
9. H. Sievert: Ueber die Zentralflaechen der Enneper'schen Flaechen konstanten Kruemmungsmasses (1886), Inaugural-Dissertation, Tuebingen, .
10. I. Sterling, H.C. Wente: Existence and classifiation of constant mean curvature multibubbletons of finite and infinite type, Indiana Univ. Math. J. 42 (1993), 1239-1266, .

Files

• Master File: DiscreteBubbleton_Master.jvx
• Applet File: DiscreteBubbleton_Master.jvx
• Preview: DiscreteBubbleton_Preview.jpg

Submission information

Submitted: Fri Oct 29 12:05:34 MET DST 2004.
Revised: Wed Oct 5 10:27:48 MET DST 2005.
Accepted: Mon Oct 31 10:29:20 CET 2005.

Authors' Addresses

University of Bath
Department of Mathematical Sciences
University of Bath
Bath, BA2 7AY
United Kingdom
u.hertrich-jeromin@maths.bath.ac.uk
http://www.maths.bath.ac.uk/~masuh/

Universitaet Muenchen
Mathematisches Institut
Theresienstr. 39
D-80333 Muenchen
Germany
hoffmann@mathematik.uni-muenchen.de
http://www.mathematik.uni-muenchen.de/personen/hoffmann.php