

 |
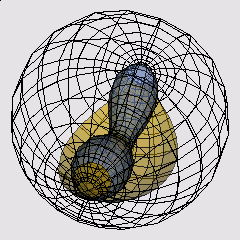
The model shows a discrete horospherical net from the 1-parameter family of a discrete Enneper net.
Discrete horospherical nets can, as discrete analogs of cmc-1 surfaces in hyperbolic space, be defined in two equivalent ways: as discrete isothermic nets with a spherical Darboux transform (which yields the hyperbolic Gauss map) or as discrete isothermic nets with a discrete minimal Calapso transform (the ``minimal cousin''), cf. [4, 5§5.7.37]. These two definitions correspond to characterizations of smooth cmc-1 surfaces in hyperbolic space by means of their isothermic transformations [3]. The equivalence of the two definitions is established by a permutability theorem for the Calapso, Darboux and Christoffel transformations for discrete isothermic nets and the fact that Calapso transforms of spherical nets are spherical [4, 5§5.7.34 and §5.7.22)].
In very much the same way as the Goursat transformation for (discrete) isothermic nets gives rise to an Enneper-Weierstrass representation for (discrete) minimal nets from (discrete) holomorphic data, these definitions provide a Bryant type representation for (discrete) horospherical nets.
More specifically: starting from a pair of dual discrete holomorphic nets in the plane, a discrete version of Bryant's linear system [1, 7] (which can be viewed as a special case of Darboux's linear system for the Darboux transformation of isothermic surfaces [2, 5§5.4.8 and §5.7.20)]) provides the Calapso transformations for one of the two holomorphic nets. Application of the Calapso transformations to this original holomorphic net provides the family of hyperbolic Gauss maps. Certain suitable Darboux transforms of these hyperbolic Gauss maps then provide the Lawson family of a (minimal) Goursat transform of the second holomorphic net (comprised of discrete horospherical nets) by a purely algebraic procedure: this is established by another permutablity theorem, which asserts that two different Darboux transforms of an isothermic net are Calapso transforms of some isothermic net and one of its Goursat transforms, cf. [5§5.7.36].
The depicted model is one of the (horospherical) nets in the Calapso (Lawson) family of a discrete Enneper surface in Euclidean space together with its hyperbolic Gauss map, which also determines the infinity boundary of the Poincare ball model of the hyperbolic ambient geometry of the net as a horospherical net in hyperbolic space. It is obtained from a square grid in the complex plane as a discrete holomorphic net and the same square grid as its dual holomorphic net. For the Lawson family of the smooth Enneper surface see [6]; a detailed description of a construction in the smooth case, similar to the one used to obtain the discrete surfaces here, is given in [5§5.6.21]; the Maple procedures that were used to produce the model are provided in the enclosed file dec.mpl.
An animation of the 1-parameter family of the discrete Enneper surface is available in the file dec_Animation.mpl, referenced below, which can be viewed with Javaview or can be imported into Maple. It shows part of the Calapso/Lawson family of the discrete Enneper surface together with the corresponding hyperbolic Gauss maps which determine the hyperbolic ambient geometry of the horospherical nets of the family, as discussed above. Note that the nets for same negative and positive values of the spectral parameter are congruent.
When approaching the (singular) value 0 of the spectral parameter the horospherical nets degenerate to a single point; if, however, the nets are appropriately rescaled then the Enneper surface is obtained in the limit: note how, for small values of the spectral parameter, the nets are very similar to the Enneper surface and how the roles of the two families of curvature lines interchange when switching the sign of the spectral parameter.
Model produced with: Maple v9, JavaView v3.94.003
| Keywords | constant mean curvature; hyperbolic space; discrete isothermic net; horospherical net; hyperbolic Gauss map; associated family; Lawson correspondence; Weierstrass representation; Bryant representation | |
| MSC-2000 Classification | 53A10 (53C42) | |
| Zentralblatt No. | 05613400 |
Submitted: Fri Oct 28 14:41:52 CEST 2005.
Revised: Tue Jun 3 10:47:51 CEST 2008.
Accepted: Tue Aug 12 14:02:57 CEST 2008.
University of Bath
Department of Mathematical Sciences
University of Bath
Bath, BA2 7AY
United Kingdom
u.hertrich-jeromin@maths.bath.ac.uk
http://www.maths.bath.ac.uk/~masuh/