

 |
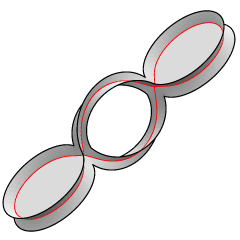
The deformation retract soap film of J. Frank Adams.
The question of exactly what minimization problem a soap film solves is a tricky one. Reifenberg [1] considered soap films to be sets that spanned a boundary in a homological sense. Adams published an appendix to [1] in which he described this soap film as an example of a set we would like to call a soap film, but which does not span its boundary in any homological sense. This film, on an unknotted wire, has a deformation retract to the wire. A retract from a set Y (the film) to a subset X (the wire) is a continuous map from Y to X which is the identity map on X. A deformation retract of Y to X is a homotopy from the identity map on Y to a retract of Y to X, with the image of the homotopy remaining in Y. It is, in fact, a strong deformation retract since the homotopy can be chosen to always be the identity map on the wire. The existence of this deformation retract shows that the soap film cannot be said to span the wire in any homological sense (at least if one stays with a wire-embedded-in-Euclidean-space model of soap films).
A Java applet in the accompanying page Retract.html can help visualize the homotopy. The homotopy starts with one of the flat disks, the left, say, retracted horizontally along the midplane to the wire, stretching the film behind it into a double layer. Then the film retracts up and down between the wire and the triple lines, sweeping out the right disk, then back over to sweep out the left disks.
Another way to visualize the deformation retract is to inverse image of each wire point in the final retract. The Java applet can also show these. Each inverse image is a curve emanating from the point and snaking around the surface until it ends in a loop. The inverse image of the wire points on the midplane also include the flat disks on their respective sides. The homotopy may be visualized as the end loops shrinking down and back along their curves to their base points on the wire.
Model produced with: Surface Evolver 2.16
| Keywords | minimal surface; deformation retract; soap film | |
| MSC-2000 Classification | 49Q20 | |
| Zentralblatt No. | 01683031 |
The Surface Evolver is available at http://www.susqu.edu/brakke/evolver. Retract.fe is the Surface Evolver input file. See comments at the start of retract.fe for instructions on evolving to the state shown here. Retract.html has a java applet (contained in Retract.jar) that illustrates the deformation retract two ways: showing the stages of the retract, and showing the inverse images of boundary points. Instructions for use are included in Retract.html.
Submitted: Mon Jan 22 09:21:14 CET 2001.
Accepted: Mon Jun 4 17:06:46 CET 2001.
Susquehanna University
Mathematics Department
Susquehanna University
Selinsgrove, PA 17870
USA
brakke@susqu.edu
http://www.susqu.edu/brakke