Unstable Discrete Minimal Graph EG-Models Home

image StableRing1_Preview.gif
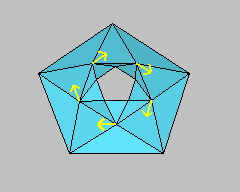
image UnstableRing_Preview.gif
image StableRing2_Preview.gif
Electronic Geometry Model No. 2001.01.044

Authors

Konrad Polthier and Wayne Rossman

Description

Two stable and an unstable discrete minimal graph over the same planar domain with the same boundary and mesh.

We define discrete compact minimal surfaces as piecewise linear continuous compact triangulated surfaces that are critical for the area functional with respect to all variations through surfaces of the same type that preserve the simplicial structure and the boundary condition (see [2] and model [5] on this server).

Although discrete minimal surfaces are critical for area, they are not necessarily area minimizing. Shown here are three discrete minimal surfaces [1] that are annular graphs over the same domain and posess the same boundary (the boundary has two components). The first and third surface is area minimizing, but the second surface is unstable and not area minimizing. In the unstable surface we include variation vectors (in yellow) at the interior vertices of the surface showing how the surface can be varied so that area decreases in second order.

The examples here are of interest because they show how discrete minimal surfaces can have properties which differ from those of smooth minimal surfaces. For example, any smooth minimal graph is uniquely determined by its boundary. Also, any smooth minimal graph is stable, see the work of Barbosa and do Carmo [3]. The examples here show that neither of these properties hold for discrete minimal surfaces.

In contrast to the existence of these counterexamples, we conjecture that the above properties of smooth minimal graphs remain true for discrete minimal graphs over simply connected convex domains. (Note that the two examples here are graphs over annular domains.)

Model produced with: JavaView version 2.00.a2

Keywords Minimal Surface; Discrete Surface; Graph; Stability
MSC-2000 Classification 53-04 (53-XX, 68Uxx, 68Rxx, 65Kxx, 65M50)
Zentralblatt No. 01683033

References

  1. Konrad Polthier and Wayne Rossman: Index of Discrete Constant Mean Curvature Surfaces (2000), Preprint 484, submitted, http://www-sfb288.math.tu-berlin.de/~konrad/articles.html.
  2. Ulrich Pinkall and Konrad Polthier: Computing Discrete Minimal Surfaces and Their Conjugates, Experimental Mathematics 2 (1993), 15--36.
  3. J. L. Barbosa and M. do Carmo: Stability of minimal surfaces and eigenvalues of the laplacian, Math. Z. 173 (1980), 13--28.
  4. Konrad Polthier and Samy Khadem and Eike Preuss and Ulrich Reitebuch: JavaView Home Page, http://www.javaview.de/.
  5. Konrad Polthier and Wayne Rossman: Discrete Catenoid (2000), Digital Model at Electronic Geometry Models, http://www.eg-models.de/2000.05.002.

Files

Submission information

Submitted: Mon Jan 22 09:21:14 CET 2001.
Revised: Fri Jul 20 11:03:03 CET 2001, Mon Aug 27 22:10:02 CET 2001.
Accepted: Tue Sep 11 15:18:14 CET 2001.

Authors' Addresses

Konrad Polthier
Technische Universität Berlin
Fachbereich Mathematik
Straße des 17. Juni 136
10623 Berlin
Germany
polthier@math.tu-berlin.de
http://www-sfb288.math.tu-berlin.de/~konrad
Wayne Rossman
Kobe University
Mathematics Department
Faculty of Science
Rokko, Kobe 657-8501
Japan
wayne@math.kobe-u.ac.jp
http://www.math.kobe-u.ac.jp/HOME/wayne/wayne.html