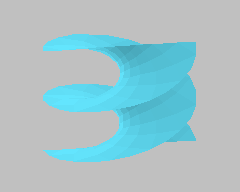Discrete Minimal Helicoid

Authors

Description

This discrete minimal helicoid extends minimally to an infinite complete discrete surface whose coordinates are given by an explicit function. This model is an example of a family of discrete helicoids. All of these helicoids have a simple explicit description of their vertices.

We define discrete compact minimal surfaces as piecewise linear continuous compact triangulated surfaces that are critical for the area functional with respect to all variations through surfaces of the same type that preserve the simplicial structure and the boundary.

This model is an explicit representation for discrete helicoids (see [1] for a proof of the representation). These discrete helicoids are a natural second nontrivial example of complete embedded discrete minimal surfaces, after the discrete catenoids (see [5]).

There exists a 4-parameter family of complete embedded discrete minimal helicoids, with the connectivity as shown in the picture. The vertices, indexed by integers i and j, are the points

x = (r Sinh(x₀ + j delta)/Sin(theta)) Cos(i theta)

y = (r Sinh(x₀ + j delta)/Sin(theta)) Sin(i theta)

z = i r

where the parameters are

• theta is strictly between 0 and Pi/2, and determines the angle between two consecutive horizontal lines.
• delta determines the horizontal spacing of the vertices.
• x₀ determines the offset of the vertices from the z-axis (if x₀=0 then the z-axis is included in the edge set)
• the homothety factor r equals the vertical distance between consecutive horizontal lines of edges.

These surfaces are invariant under the screw motion that combines vertical upward translation of distance 2 r with rotation about the z-axis by an angle of 2 theta. All helicoids of this family interpolate smooth helicoids since the horizontal vertices lie on straight lines and the vertical twist and distance of adjacent lines are constant.

The helicoids are comprised of planar quadrilaterals, each triangulated by four coplanar triangles. Each quadrilateral is the vertex star of a unique vertex whose position within the quadrilateral may be arbitrarily choosen. In this model the position of this vertex was choosen to avoid a case distinction in the formula. None of its four boundary edges of the quadrilateral are vertical or horizontal, and one pair of opposite vertices in its boundary have the same z-coordinate, and the four boundary edges consist of two pairs of adjacent edges so that within each pair the adjacent edges are of equal length.

Note, the helicoids are not directly discrete conjugates of the discrete catenoids [5] since the discrete conjugate surfaces of a conforming triangulation is a non-conforming triangulation as described in [6].

Model produced with: JavaView 2.04.001

References

1. Konrad Polthier and Wayne Rossman: Index of Discrete Constant Mean Curvature Surfaces (2000), Preprint 484, submitted, http://www-sfb288.math.tu-berlin.de/~konrad/articles.html.
2. Ulrich Pinkall and Konrad Polthier: Computing Discrete Minimal Surfaces and Their Conjugates, Experimental Mathematics 2 (1993), 15--36.
3. Bernd Oberknapp and Konrad Polthier: An Algorithm for Constant Mean Curvature Surfaces, in Hans-Christian Hege and Konrad Polthier (Eds.): Visualization and Mathematics, Springer Verlag (1997), 141--161.
4. Konrad Polthier and Samy Khadem and Eike Preuss and Ulrich Reitebuch: JavaView Home Page, http://www.javaview.de/.
5. Konrad Polthier and Wayne Rossman: Discrete Catenoid (2000), Digital Model at Electronic Geometry Models, http://www.eg-models.de/2000.05.002.
6. Konrad Polthier: Conjugate Harmonic Maps and Minimal Surfaces (2000), Preprint 446, submitted, http://www-sfb288.math.tu-berlin.de/~konrad/articles.html.

Files

• Master File: Helicoid_Master.jvx
• Applet File: Helicoid_Master.jvx
• Preview: Helicoid_Preview.gif
• Other: Helicoid_Display.jvd

Submission information

Submitted: Mon Jan 22 09:21:14 CET 2001.
Revised: Thu Aug 30 14:51:35 CET 2001, Mon Aug 27 21:23:20 CET 2001.
Accepted: Tue Sep 11 15:20:29 CET 2001.

Authors' Addresses

Technische Universität Berlin
Fachbereich Mathematik
Straße des 17. Juni 136
10623 Berlin
Germany
polthier@math.tu-berlin.de
http://www-sfb288.math.tu-berlin.de/~konrad

Kobe University
Mathematics Department
Faculty of Science
Rokko, Kobe 657-8501
Japan
wayne@math.kobe-u.ac.jp
http://www.math.kobe-u.ac.jp/HOME/wayne/wayne.html