A discrete TT surface EG-Models Home

image TTsurface_Preview.gif
image TTsurface_Extended_Preview.gif
image Schwarz_Preview.gif
Electronic Geometry Model No. 2005.04.001

Author

Matthias Nieser

Description

This is a family of discrete minimal surfaces given by an explicit formulation for the position of its vertices. It is a discrete variant of the smooth TT surface described by Karcher [1] which is a minimal surface bounded by two equilateral triangles in parallel planes and in twisted positions relative to each other.

A discrete minimal surface is a triangulated piecewise linear simplicial surface. It is critical for its surface area with respect to variations of the position of the inner vertices as defined in [2].

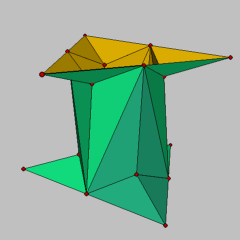
This surface is constructed using a surface patch consisting of five vertices vi, i=0..4 and four triangles Ti=(v0, vi, vi+1), i=1..4 with v5:=v0. The explicit coordinates of the vertices are up to a scaling factor given by:

v0 = (0, 3-1/sqrt(h2/12+1/3), h/(4 sqrt(h2/12+1/3))),
v1 = (0, 0, 0),
v2 = (sqrt(3), 3, 0),
v3 = (0, 2, h),
v4 = (-sqrt(3), 3, 0)

with a height parameter h>0. The shown models have height h=5.

A calculation of the area gradient at the inner vertex v0 shows that this surface patch is a minimal surface.

In a second step, reflect the whole geometry across the plane {(x,y,h/2) | x,y in R} and rotate the reflected geometry around the z axis by 60 degrees. The result is a second surface which joins the original surface at the vertices v2 and v3. Repeat the reflection and rotation until 6 surface patches are obtained. They arrange to a discrete minimal surface which is bounded by two twisted triangles as the smooth TT surface is (figure 1).

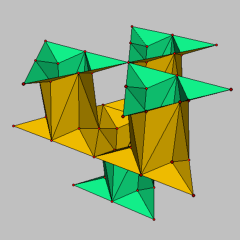
The second figure shows how the discrete TT surface can be extended by rotation about the outer edges to a triply periodic discrete minimal surface.

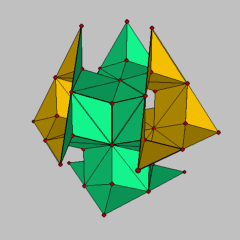
In the special case h=2 sqrt(2), the TT surface gets additional symmetries. Pairs of adjacent triangles become planar quadrilaterals and the geometry becomes a discrete variant of the Schwarz D surface. A fundamental part of this triply periodic surface is shown in figure 3. By swapping each planar edge in the quadrilaterals, one gets a discrete minimal surface, which was constructed by Rossman [5] and called a discrete variant of the superman surface.

Some likewise constructed discrete minimal surfaces are given in [5] (Rossman), e.g. discrete versions of the Schwarz CLP surface or H surface from Schoen. Polthier and Rossman [4] presented an explicit description of a family of discrete catenoids and helicoids.

Model produced with: JavaView 3.80

KeywordsTT surface; Minimal surface; Discrete surface
MSC-2000 Classification53-04 (53-XX, 68Uxx, 68Rxx, 65Kxx, 65M50)
Zentralblatt No.05264903

References

  1. H. Karcher: The triply periodic minimal surfaces of Alan Schoen and their constant mean curvature companions, Manuscripta Math. 64 (1989), 291--357, .
  2. U. Pinkall and K. Polthier: Computing Discrete Minimal Surfaces and Their Conjugates, Experimental Mathematics 2 (1993), 15--36, .
  3. K. Polthier, K. Hildebrandt, E. Preuss and U. Reitebuch: JavaView Homepage, http://www.javaview.de/.
  4. K. Polthier and W. Rossman: Index of Discrete Constant Mean Curvature Surfaces, J. Reine und Angew. Math. (Crelle Journal) 549 (2002), 47--77, .
  5. W. Rossman: Infinite periodic discrete minimal surfaces without selfintersections, eprint arXiv:math/0410314 (10/2004), .

Files

Submission information

Submitted: Fri Apr 8 14:09:40 CEST 2005.
Revised: Thu Jun 2 13:05:42 CEST 2005, Wed Jun 8 13:12:35 MET DST 2005.
Accepted: Mon Jul 4 13:49:28 MET DST 2005.

Author's Address

Matthias Nieser
Zuse Institute Berlin
Takustrasse 7
D-14195 Berlin, Germany
nieser@zib.de
http://www.zib.de/nieser