

 |
 |
 |
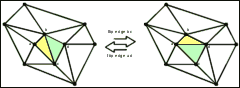
A counter example that shows that local flips in triangulated surfaces do not always lead to global optimal triangulations.
The surface of a 3D object is often represented by triangular faces, i.e. as a triangulation of its vertices. A common method to modify and optimize the surface are local edge flips. A flip of the joint edge bc of two adjacent triangles abc and cbd replaces these triangles by the triangles abd and adc with the new joint edge ad. The flip operation is only considered when it does not lead to a self intersecting surface, i.e. the surface has to stay homeomorph to a sphere.
Given a triangulation of a set of points in the plane, an edge e is flippable if the two adjacent triangles form a convex quadrilateral. It is a well-known fact, that all possible triangulations of a given point set in the plane, can be reached by a sequence of flip operations.
Given a surface triangulation of a set of points in 3-space, an edge e is flippable if the two new adjacent triangles abd and adc are not intersect with any of the existing edges and if the new edge ad does not yet exist in the triangulation. Note that flipping a reflex edge can be seen as adding a tetrahedron to the surface, while flipping a convex edge does the reverse.
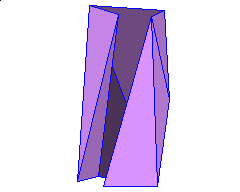
A basic question is whether any two possible surfaces of a given point set are connected by these flip operations. In other words, is it always possible to transform one triangulation of a point set to another by a finite sequence of flip operations? The answer is NO, as can be shown by this polyhedron.*
The construction of the polyhedron can be found in a paper by Aichholzer, Alboul and Hurtado [1]. The 10 polyhedron vertices are in general and convex position and the surface consists of 16 triangles in general position. A detailed analysis [1] shows that there are only four flippable edges. Trying to flip one of the other edges would result in a triangulation where the new inserted edge either already exists or at least one of the two new triangles intersects with at least one of the existing triangles. Since some of the flippable edges block each other and no one of the not flippable edges becomes flippable, there are only 9 different triangulated surfaces reachable. You can examine this by exploring it interactively and flip the polyhedron at [2] (see also the link to Flip-disconnected_Polyhedron.html below).
Some reflex edges of the initial surface are part of all 9 reachable triangulations. Therefore the convex hull of the vertices can not be reached by local flips. (Recall that the convex hull is a valid surface because the vertices lie in convex position)
Combining the results the following theorem holds:
Theorem 1: Given a set V of vertices in 3D, the class of triangulated surfaces with vertex set V is not connected by the flip operation, even if V is in general and convex position.
* Due present limitations of JavaView, the polyhedron may not be shown correctly. Alternatively please try [2] (or the link to Flip-disconnected_Polyhedron.html below), which in addition allows to flip edges of the polyhedron.
Model produced with: JavaView v.2.14
| Keywords | surface; triangulation; flip | |
| MSC-2000 Classification | 52B10 (14Q10) | |
| Zentralblatt No. | 05264886 |
Use "Flip-disconnected_Polyhedron.html" to explore the polyhedron and inspect flippable edges. "3D_Applet.jar" is the archive in which the used JAVA-Applet is stored. The Adobe Acrobat Document "3D_Applet Introduction.pdf" contains additional information on how to use the applet for your own objects.
Submitted: Wed Jan 30 09:53:21 GMT 2002.
Revised: Thu May 23 09:52:16 GMT 2002.
Accepted: Fri Sep 27 15:46:02 CEST 2002.
Graz University of Technology
Stremayrgasse 6/4/19
8010 Graz
Austria
moserw@gmx.at