Triply periodic minimal surfaces of genus 4

Authors

Description

It is known that any compact minimal surface in a flat 3-torus can be regarded as a triply-periodic minimal surface in Euclidean 3-space, and here we exhibit such a surface.

For a minimal surface in a flat 3-torus, we can consider a one-parameter family of isometric minimal surfaces. Locally this family is actually the associate family (as surfaces in Euclidean 3-space), but we reserve the phrase "associate surface" to mean only those surfaces in the family that are well-defined in some torus, noting it is possible that such surfaces might not be well-defined in any torus. Thus we make the following definition: If some member of this family is well-defined in some torus, we call it an associate surface of the original one. Nagano and Smyth [3] gave a criterion for the existence of associate surfaces. Namely, every element of the one parameter family of isometric minimal surfaces is either an associate surface or else is dense in Euclidean 3-space.

In [2], Meeks introduced the following notation: a minimal surface in a flat 3-torus satisfies property P if the associate surfaces contain a countable dense subset in the set of all isometric minimal surfaces of the original minimal surface.

In [6], the second author constructed a new example of a minimal surface into a flat torus which satisfies property P. This surface is defined on a trigonal Riemann surface of genus 4. Note that several examples which satisfy property P and have the linear symmetries of a cube (the expression "linear symmetries of a cube" is precisely defined in [2]) are known: for example, Schwarz surfaces [5] and A. Schoen's surfaces [4]. However, our trigonal minimal surface does not have the linear symmetries of a cube.

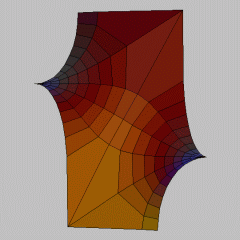
The following are shown here: 1) a piece of the fundamental piece of the surface, which is bounded by six planar geodesics, and 2) the fundamental piece of the surface for the translational symmetry group, which consists of twelve copies of the first piece, produced by reflections along planar geodesics.

A more detailed description of this surface can be found in the pdf file included in this model.

Model produced with: JavaView v.3.84

References

1. D. Hoffman and H. Karcher: Complete embedded minimal surfaces of finite total curvature, Geometry V , Encyclopaedia Math. Sci. Springer 90 (1997), 5-93.
2. W. H. Meeks III: The theory of triply periodic minimal surfaces , Indiana Univ. Math. J. 39 (1990), 877-935.
3. T. Nagano and B. Smyth: Periodic minimal surfaces, Comment. Math. Helvetici 53 (1978), 29-55.
4. A. Schoen: Infinite periodic minimal surfaces without self-intersections, Technical Note D-5541, N.A.S.A. Cambridge, Mass. (1970).
5. H. A. Schwarz: Gesammelte Mathematische Abhandlungen, Springer-Verlag, Berlin (1890).
6. T. Shoda: New components of the Moduli space of minimal surfaces in 4-dimensional flat tori, J. London Math. Soc. 70 (2004), 797-816.

Files

• Master File: shoda1_Master.jvx
• Master File: shoda2_Master.jvx
• Applet File: shoda1_Applet.jvx
• Applet File: shoda2_Applet.jvx
• Preview: shoda1_Preview.gif
• Preview: shoda2_Preview.gif
• Other: shoda.pdf

Submission information

Submitted: Fri Oct 14 13:08:36 CEST 2005.
Revised: Mon Feb 20 11:26:16 CET 2006.
Accepted: Tue Oct 17 10:15:00 CEST 2006.

Authors' Addresses

Kobe University
Mathematics Department
Faculty of Science
Rokko, Kobe 657-8501
Japan
fujimori@math.kobe-u.ac.jp
http://www.math.kobe-u.ac.jp/~fujimori

Kyushu University
Faculty of Mathematics
Hakozaki, Fukuoka 812-8581
Japan
tshoda@math.kyushu-u.ac.jp
http://www.math.titech.ac.jp/~tshoda/welcome-e.html