

 |
 |
 |
Surfaces made from a constant mean curvature (CMC) H surface by moving in the normal direction a distance of 1/(2H) and 1/H, respectively, are of constant Gaussian curvature K=4H^2 and of constant mean curvature -H, respectively. We call them the parallel K-surfaces and parallel H-surfaces, respectively. In this model, we study CMC surfaces whose parallel H-surfaces are congruent to the original surface. In particular, we show that Delaunay surfaces -- and the simplest Wente tori -- are surfaces of this type.
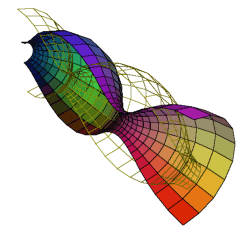
The locus of a focus of an ellipse as the ellipse is rotated without slippage along a straight line in a plane forms a curve that is called an undulary. (Here one can imagine a wheel in the shape of an ellipse rolling along a road.) The locus of a focus of a hyperbola as the hyperbola is rotated without slippage along a straight line in a plane forms a curve which is called a nodary. Rotating each of the roulettes about the straight line used to construct them produces surfaces with constant mean curvature in Euclidean three-space, called Delaunay surfaces: unduloids (by rolling an undulary), and nodoids (by rolling a nodary). Delaunay surfaces can represented in terms of elliptic integrals, and they are periodic in the direction of the axis. (See [1].)
In the first two figures, we see pieces of unduloids and nodoids, along with their parallel H-surfaces. We see that the parallel H-surfaces are simply the original surfaces, translated along the axis by half the translational period of the surfaces.
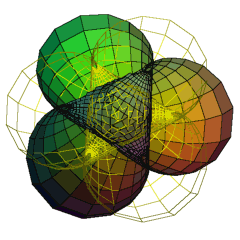
Hopf conjectured that the only closed CMC surface in Euclidean three-space is a round sphere. This is true if the surface is assumed to be either genus 0 or embedded, but in general it is false, and the first counterexamples (with genus 1) were found by Wente. One can give explicit formulas in terms of theta functions for these original Wente tori and their parallel H-surfaces (see [2], for example).
In the final figure, we see an original Wente torus and its parallel H-surface. Note that the parallel H-surface differs from the original Wente surface by a rotation about the surfaces' central axis with angle half the angle of the surfaces' rotational symmetry.
We note that there are geometric similarities between the relationship of Delaunay surfaces with their parallel H-surfaces and the relationship of original Wente tori with their parallel Wente tori.
If a CMC H surface, call it S, has a plane of reflection symmetry, then the parallel H-surface of S has the same reflection symmetry. Thus, if S is a surface of revolution, the parallel H-surface is also a surface of revolution about the same axis. Furthermore, if S has a translational period along the axis of revolution, the parallel H-surface has the same translational period. Since Delaunay surfaces (for a given fixed H) are uniquely determined by the length of their translational periods, it follows that a Delaunay surface is congruent to its parallel H-surface. Please see the postscript (or pdf) file included in this model for a detailed proof that Delaunay surfaces are congruent to their parallel H-surfaces. The postscript file also contains a proof that the original Wente tori are congruent to their parallel H-surfaces. Please also see the included Mathematica files for making figures, and the final jvx file for a full Wente torus.
Model produced with: JavaView v.2.13.002
| Keywords | constant mean curvature surface; parallel surface; surface of revolution; Delaunay surface; Wente torus | |
| MSC-2000 Classification | 53A10 (53C42) | |
| Zentralblatt No. | 05264889 |
Submitted: Fri Mar 8 09:19:28 CET 2002.
Revised: Thu Jul 22 14:30:40 CEST 2004.
Accepted: Sat Sep 4 11:23:39 GMT 2004.
Kobe University
Department of Mathematics
Graduate School of Science and Technology
Rokko, Kobe 657-8501
Japan
kentatoyama@mail.goo.ne.jp